peterpops
Junior Member level 3
Hi!
I'm doing some exercises in Microelectronic Circuits (Sedra Smith 5th ed) and got stuck on 1.13 (voltage amplifiers)
NOTE! This is not the end-chapter excercises included in the PDF solution manual!
According to SedraSmith a voltage amplifier can be modeled as in the figure.
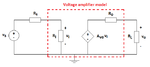
The question is:
"An amplifier with a voltage gain of +40 dB, an input resistance of 10kΩ, and an output resistance of 1kΩ is used to drive a 1-kΩ load. What is the value of Avo? Find the value of power gain in dB"
The answer in the book is:
"Ans. 100 V/V; 44 dB"
My solution:
I know
Voltage gain in dB = 40, which means 40 = 20 log(Av) => Av = 100
EQ.1: \[{A}_{v}=\frac{{v}_{o}}{{v}_{i}}=100\]
Voltage division gives me \[{v}_{o}={A}_{vo}{v}_{i}\left(\frac{{R}_{L}}{{R}_{L}+{R}_{o}}\right)\]
rewritten \[{A}_{vo}=\left(\frac{{v}_{o}}{{v}_{i}}\right)\left(\frac{{R}_{L}+{R}_{o}}{{R}_{L}}\right)=100\left(\frac{{R}_{L}+{R}_{o}}{{R}_{L}}\right)\]
From here I can go 2 ways:
1. Since I know Ro and RL I just substitute them in the equation above and the answer is \[{A}_{vo}=100\left(\frac{1000+1000}{1000}\right)=200\]
Or
2. Avo is the "open-circuit voltage gain" which means I assume that RL is infinite which gives me \[{A}_{vo}=100\]
Since the answer is 100 V/V I assume solution 2 is the correct one.
Now over to the second part of the question, the power gain in dB.
The current through Ri is (with the help of EQ.1) \[{i}_{i}=\frac{{v}_{i}}{{R}_{i}}=\frac{{v}_{o}}{{100R}_{i}}\]
The current through Ro is \[{i}_{o}=\frac{{v}_{o}}{{R}_{L}}\]
Which gives me the current gain \[{A}_{i}=\frac{{i}_{o}}{{i}_{i}}=\frac{\frac{{v}_{o}}{{R}_{L}}}{\frac{{v}_{o}}{{100R}_{i}}}=\frac{{100R}_{i}}{{R}_{L}}\]
With values inserted Ai = 1000 A/A
Power gain, Ap = Av*Ai and depending on which voltage gain solution above
Ap = 200 * 1000 = 200000, or Ap = 100 * 1000 = 100000
in dB the power gain is either = 10*log(200000) = 53dB, or = 10*log(100000) = 50dB
So where did I go wrong or is the SedraSmith answer incorrect?
Thanks in advance
/P
I'm doing some exercises in Microelectronic Circuits (Sedra Smith 5th ed) and got stuck on 1.13 (voltage amplifiers)
NOTE! This is not the end-chapter excercises included in the PDF solution manual!
According to SedraSmith a voltage amplifier can be modeled as in the figure.

The question is:
"An amplifier with a voltage gain of +40 dB, an input resistance of 10kΩ, and an output resistance of 1kΩ is used to drive a 1-kΩ load. What is the value of Avo? Find the value of power gain in dB"
The answer in the book is:
"Ans. 100 V/V; 44 dB"
My solution:
I know
Voltage gain in dB = 40, which means 40 = 20 log(Av) => Av = 100
EQ.1: \[{A}_{v}=\frac{{v}_{o}}{{v}_{i}}=100\]
Voltage division gives me \[{v}_{o}={A}_{vo}{v}_{i}\left(\frac{{R}_{L}}{{R}_{L}+{R}_{o}}\right)\]
rewritten \[{A}_{vo}=\left(\frac{{v}_{o}}{{v}_{i}}\right)\left(\frac{{R}_{L}+{R}_{o}}{{R}_{L}}\right)=100\left(\frac{{R}_{L}+{R}_{o}}{{R}_{L}}\right)\]
From here I can go 2 ways:
1. Since I know Ro and RL I just substitute them in the equation above and the answer is \[{A}_{vo}=100\left(\frac{1000+1000}{1000}\right)=200\]
Or
2. Avo is the "open-circuit voltage gain" which means I assume that RL is infinite which gives me \[{A}_{vo}=100\]
Since the answer is 100 V/V I assume solution 2 is the correct one.
Now over to the second part of the question, the power gain in dB.
The current through Ri is (with the help of EQ.1) \[{i}_{i}=\frac{{v}_{i}}{{R}_{i}}=\frac{{v}_{o}}{{100R}_{i}}\]
The current through Ro is \[{i}_{o}=\frac{{v}_{o}}{{R}_{L}}\]
Which gives me the current gain \[{A}_{i}=\frac{{i}_{o}}{{i}_{i}}=\frac{\frac{{v}_{o}}{{R}_{L}}}{\frac{{v}_{o}}{{100R}_{i}}}=\frac{{100R}_{i}}{{R}_{L}}\]
With values inserted Ai = 1000 A/A
Power gain, Ap = Av*Ai and depending on which voltage gain solution above
Ap = 200 * 1000 = 200000, or Ap = 100 * 1000 = 100000
in dB the power gain is either = 10*log(200000) = 53dB, or = 10*log(100000) = 50dB
So where did I go wrong or is the SedraSmith answer incorrect?
Thanks in advance
/P