shaiko
Advanced Member level 5
- Joined
- Aug 20, 2011
- Messages
- 2,644
- Helped
- 303
- Reputation
- 608
- Reaction score
- 297
- Trophy points
- 1,363
- Activity points
- 18,302
Lets examine the following daisy chain scheme (assuming a lossless system):
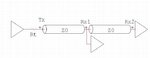
The facts:
Propogation delay from Tx to Rx1 is 50nS.
Propogation delay from Tx to Rx2 is 100nS.
Hence, the propogation delay from Rx1 to Rx2 is 50nS.
Impedances of Rt and Z0 are matched.
At Time = 0 a 5V step signal is sent accross the line.
The voltage accross point Tx, at Time = 0 is:
V(Tx) = ( 5V * Z0 ) / ( Z0 + Rt )
I know the voltage across point Rx1 at Time = T will be 2.5V. But I don't understand why...
Shouldn't the wave bounce back from Rx1 and double to 5V at the same moment it hits? (because of the ~infinite impedance of the driver...)
The facts:
Propogation delay from Tx to Rx1 is 50nS.
Propogation delay from Tx to Rx2 is 100nS.
Hence, the propogation delay from Rx1 to Rx2 is 50nS.
Impedances of Rt and Z0 are matched.
At Time = 0 a 5V step signal is sent accross the line.
The voltage accross point Tx, at Time = 0 is:
V(Tx) = ( 5V * Z0 ) / ( Z0 + Rt )
I know the voltage across point Rx1 at Time = T will be 2.5V. But I don't understand why...
Shouldn't the wave bounce back from Rx1 and double to 5V at the same moment it hits? (because of the ~infinite impedance of the driver...)
