Julian18
Full Member level 3
Hi, there
I am now reading a paper named "The Yin-Yang of Matching: Part 2—Practical Matching Techniques" by Randy Rhea, In the second section, the paper presents formula for general transmission line transformer, and I quoted here
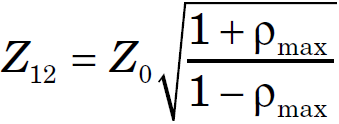
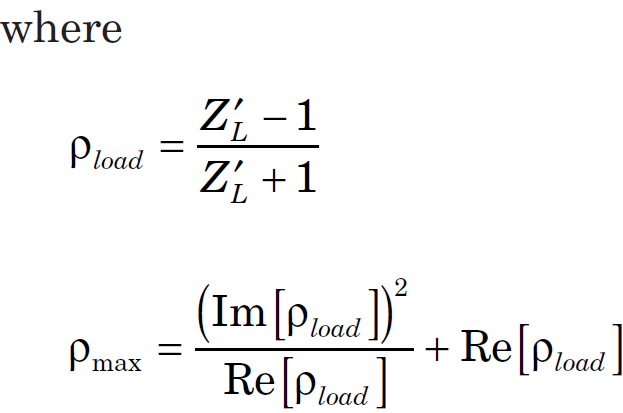
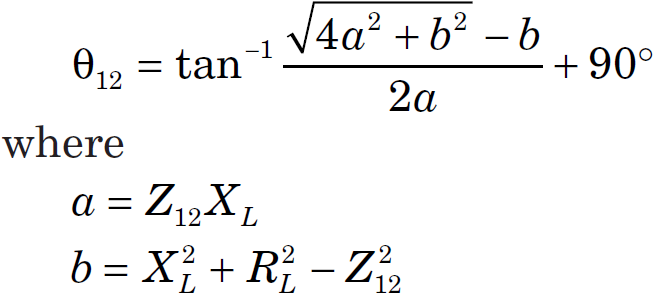 I can not find the way to derive these two formula, can anybody give me a clue?
I can not find the way to derive these two formula, can anybody give me a clue?
also I upload the original paper, if any of you guys may need.
Thanks
Julian
I am now reading a paper named "The Yin-Yang of Matching: Part 2—Practical Matching Techniques" by Randy Rhea, In the second section, the paper presents formula for general transmission line transformer, and I quoted here
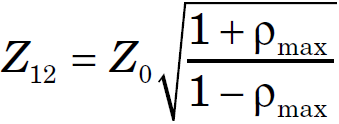
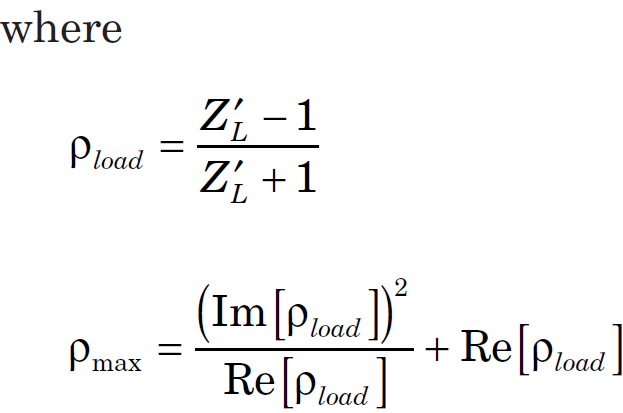
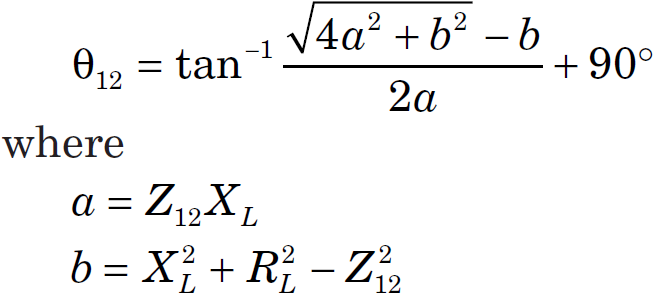
also I upload the original paper, if any of you guys may need.
Thanks
Julian