maxplanck
Newbie level 6
Hello friends,
How can I calculate a 3-Phase Full Wave Bridge Rectifier Circuit currents? I added an image. Isolation transformer is connect Delta-Delta. I want to calculate other currents according to I load.
(
I load = DC load current,
I d1 = I d2 = I d3 = DC diode currents,
I s1 = I s2 = I s3 = Transformer Secondary RMS currents,
I p1 = I p2 = I p3 = Transformer Primary RMS currents,
)
Thank you,
Regards.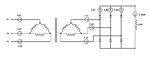
How can I calculate a 3-Phase Full Wave Bridge Rectifier Circuit currents? I added an image. Isolation transformer is connect Delta-Delta. I want to calculate other currents according to I load.
(
I load = DC load current,
I d1 = I d2 = I d3 = DC diode currents,
I s1 = I s2 = I s3 = Transformer Secondary RMS currents,
I p1 = I p2 = I p3 = Transformer Primary RMS currents,
)
Thank you,
Regards.

Last edited: