[Theoretical Question] Long data sequence filtering

[camancunian]

Hi all,
I have a question related to filtering a long data using FFT convolution.
To start, let me explain my understanding about convolution in time domain.
Let x is time domain long input signal that has L points.
Let h is time domain filter kernel that has M points.
The length of y will be N=L+M-1 if y = x*h, i.e. y is the output of convolution between x and h in time domain.

The length of y will also be N=L+M-1 if we use N-FFT convolution instead.
Let N=L+M-1 and N fortunately is the power of two.
First, we zero padded the input x and filter kernel h so that both have length of N points.
Second, take N-FFT of zero padded-x and h and multiply them, yielding output Y in frequency domain.
Third, take N-IFFT to produce y that has N=L+M-1 points.

The problem arises if I segment the long data x to be small blocks and filter them independently (here the filter is same for all blocks).
Refer to a book by Proakis (DSP: Principles, algorithms, and application 3rd edition, page 430-433), there are two methods for doing so: overlap-save method and overlap-add method.

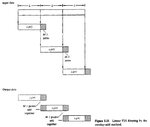
I clearly understand about how overlap-add method works. It simply yields the overall filtered output y that has length L+M-1 points. Each filtered output block will extend M-1 points to the right since we have added the input block by M-1 zeros. By overlapping addition the most right block will extend to the right by M-1 points and these points that make the overall filtered output y has M-1 point-extension.

My problem is about overlap-save method.
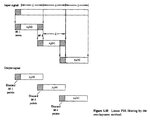
The key procedure is just for the first block we define the most left M-1 points to be zeros, while the other blocks gather the most left M-1 points from the previous block. It is shown that using this method the overall filtered output y will have length of L, which is confusing. I bet this is because we define M-1 points at x(-1:M-1) to be zeros (something that we don't bother in overlap-add method). This definition has consequence of deletion of the most left M-1 points of the overall filtered signal y (due to deletion of the most left M-1 points of each block).

If discarding the most left M-1 points in overlap-save method is allowed, it is logical to neglect the most right M-1 points in overlap-add method. However, why is it not the case ?

Hope you all shed light on my problem or give recommendation books to read about this particular difficulty. Thanks in advance.

 

[camancunian]

So sad there is no one who replies this thread.
However, I have got the answer.
For overlap-save method, we need to be aware that the attached figure is misleading. We need to make sure that the last block needs to have zero-valued for at least the most right M-1 points, otherwise take another block and extend it to be zeros for the undefined points.

Cheers

 

[D.A.(Tony)Stewart]

maybe this will help