spectrallypure
Member level 3
Load seen by opamp in non-inverting config. is TWICE w.r.t. inverting config.?
Hi! I've come across the result that the load seen by an opamp is radically different depending if it's in inverting or non-inverting configuration. I wonder if I'm making some mistake, or if it's a well known fact and I was just ignorant.
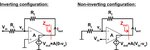
Considering the figures in attachment (resistive feedback and no explicit load are considered for simplicity):
For the inverting configuration:
Vout/Vin = -A.Rf/[Rf+Ri(1+A)] --> -Rf/Ri for large A
Iout/Vin = -(1+A)/[Rf+Ri(1+A)] --> -1/Ri for large A
Rout = Vout/Iout = Rf(A)/(1+A) --> Rf for large A
For the non-inverting configuration:
Vout/Vin = A(Ri+Rf)/[Rf+Ri(1+A)] --> 1+Rf/Ri for large A
Iout/Vin = A/[Rf+Ri(1+A)] --> 1/Ri for large A
Rout = Vout/Iout = Ri+Rf for ANY value of A!
Thus, the load seen by the opamp in the non-inverting configuration is much larger than in the inverting case (e.g. twice as much, assuming Rf=Ri). Can someone please confirm if this is correct (a reference to a book or paper showing this would be GREATLY appreciated), or if there is a mistake?
Thanks in advance!
Hi! I've come across the result that the load seen by an opamp is radically different depending if it's in inverting or non-inverting configuration. I wonder if I'm making some mistake, or if it's a well known fact and I was just ignorant.
Considering the figures in attachment (resistive feedback and no explicit load are considered for simplicity):
For the inverting configuration:
Vout/Vin = -A.Rf/[Rf+Ri(1+A)] --> -Rf/Ri for large A
Iout/Vin = -(1+A)/[Rf+Ri(1+A)] --> -1/Ri for large A
Rout = Vout/Iout = Rf(A)/(1+A) --> Rf for large A
For the non-inverting configuration:
Vout/Vin = A(Ri+Rf)/[Rf+Ri(1+A)] --> 1+Rf/Ri for large A
Iout/Vin = A/[Rf+Ri(1+A)] --> 1/Ri for large A
Rout = Vout/Iout = Ri+Rf for ANY value of A!
Thus, the load seen by the opamp in the non-inverting configuration is much larger than in the inverting case (e.g. twice as much, assuming Rf=Ri). Can someone please confirm if this is correct (a reference to a book or paper showing this would be GREATLY appreciated), or if there is a mistake?
Thanks in advance!
