Selection of values for Underdamped Second order low pass filter

[mamech]

Hello everyone

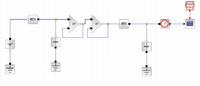
I want to design a second order low pass filter, but I need to select values of resistances and capacitances so I get underdamped oscillation for a step input.

I have read that this can be done using RLC circuit, but I want to design it using two cascaded RC first order filters, but i could not manage to do this. As I understand, the matter is just a selection of parameters for having damping ratio < 1 , but I could not get any values that achieve the goal.

I wonder, is it possible to design a second order filter using two RC circuits while making the system underdamped??

 

[FvM]

This are two cascaded first order filters which have real poles and can't show an oscillating step response by nature. Instead you'll want a second order filter with a complex pole pair. It can be implemented either as LC filter or as active filter with feedback. Some references are here https://en.wikipedia.org/wiki/Active_filter

You'll decide for a specific cutoff frequency, filter Q and a circuit topology, then use any of the filter design tools on the internet to calculate the R and C values.

 

[mamech]

hmmm yes, now I got it . the transfer function of a cascaded RC second order Low pass filter is by nature 1/((T1S+1)(T2S+2))
so it can be either over damped or critically damped, but it will never oscillates because these 2 poles are always real.

 

[LvW]

hmmm yes, now I got it . the transfer function of a cascaded RC second order Low pass filter is by nature 1/((T1S+1)(T2S+2))
so it can be either over damped or critically damped, but it will never oscillates because these 2 poles are always real.

Yes - correct.
But with the componenets you have used in your circuit you can realize a second-order RC filter in Sallen-Key configuration (search for "unity-gain Sallen-Key").
All you need is some feedback. So you can implement pole damping (Q values) as you like.

- - - Updated - - -

If you want (or can afford) to use two buffers (by the way: Two buffers in series are meaningless) do the following:
* Place one of the buffers at the output of the 2nd RC section ;
* Connect the output of this buffer to the first capacitor (instead of grounding it) thus realizing signal feedback.
* Then, the following formulas apply for two equal capacitors C1=C2=C and R2=k*R1 (R1 is the resistor of the first RC section):

Pole frequency wp=1/[R1*C*sqrt(k)]
Pole quality factor Qp=sqrt(1/k)
Qp=1/(2*d) with d=damping factor.

Note: Using this two-opamp topology you have simplified formulas if compared with the single-OP Sallen-Key structure.

 

[Audioguru]

A Sallen-Key filter with equal resistor and capacitor values will have a Butterworth response when its gain is 1.586 and will oscillate when its gain is about 2.0 and higher. Try it with a gain of 1.8 times.

 

[LvW]

A Sallen-Key filter with equal resistor and capacitor values will have a Butterworth response when its gain is 1.586 and will oscillate when its gain is about 2.0 and higher. .

For this single-opamp unity gain Sallen-Key filter the Pole Q is Qp=1/(3-Acl) with the closed-loop gain Acl.
That means: For a gain of Acl=2 we have Qp=1. Hence, the circuit is stable and will not oscillate (oscillation condition: Qp=infinity for Acl=3).