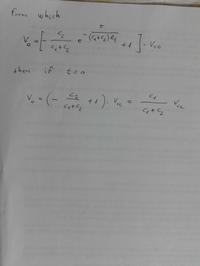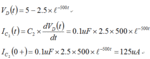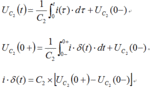Johnny_YU
Member level 2

- Joined
- Oct 17, 2013
- Messages
- 45
- Helped
- 2
- Reputation
- 4
- Reaction score
- 2
- Trophy points
- 8
- Activity points
- 371
HI all
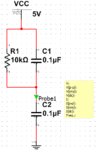
I'm trying to analyse a simple RC circuit.
Condition: the initial energy stored in this simple RC circuit is ZERO.
AT t=0s ,a DC voltage source of 5 Volts is applied to the circuit.
I need to find the Transient Response of Vd.
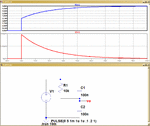
I did the calculations, the result indicates that when t=0s , Vd approaches to 5Volts.
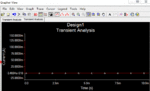
And then I use 'Multisim 12' to do a Transient Response simulation for Vd, the result indicates that when t=0s, Vd approaches to 2.5Volts.
So, which One is Correct? Is there anything wrong with the Calculations or the Simulation?
Thanks!

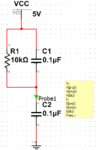

I'm trying to analyse a simple RC circuit.
Condition: the initial energy stored in this simple RC circuit is ZERO.
AT t=0s ,a DC voltage source of 5 Volts is applied to the circuit.
I need to find the Transient Response of Vd.
I did the calculations, the result indicates that when t=0s , Vd approaches to 5Volts.
And then I use 'Multisim 12' to do a Transient Response simulation for Vd, the result indicates that when t=0s, Vd approaches to 2.5Volts.
So, which One is Correct? Is there anything wrong with the Calculations or the Simulation?
Thanks!