seeker13
Junior Member level 1

- Joined
- May 18, 2013
- Messages
- 17
- Helped
- 0
- Reputation
- 0
- Reaction score
- 0
- Trophy points
- 1,281
- Activity points
- 1,534
I thought I know the basic of OPAMPs and MOSFETs, so I tried designing a simple regulator, but the voltage measurement goes against all I know. I would be really grateful if someone would enlighten me about the behavior of this circuit.
In a nutshell:
---------------
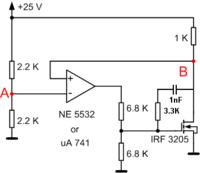
I measure very large voltage difference between A and B (more than hundreds mV, up to 1V) - shouldn't it be very small (up to few mV)?
More detailed explanation:
--------------------------------
I implemented a negative feedback via non-inverting input of OPAMP, and the voltages on OPAMP inputs (points A and B) differ by more than 500 mV. AFAIK, both points A and B should be about 12.5V, and the difference shouldn't be more than a few mV (at worst few dozen mV - maximum input offset voltage). What I measure is 12.7V at point A, but 13.4V at B!?
I thought maybe it was faulty chip (uA 741), so I tested with another one, even tried with other type of OPAMPs (NE 5532 and LM 358) - the large difference between inputs was still there. One other strange thing: when I connected a few more MOSFETs in parallel with the one shown here, the difference of input voltages changed with every MOSFET I added?
One final remark: in attempt to debug the problem, I reduced the circuit to the one shown here (what I actually tried to do was a power supply), and the behavior I just described pertains to this simple circuit.
Is someone has an idea why the voltages at points A and B differ so much, I'd love to hear it. Thanks!
In a nutshell:
---------------
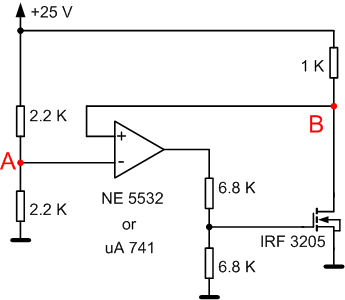
I measure very large voltage difference between A and B (more than hundreds mV, up to 1V) - shouldn't it be very small (up to few mV)?
More detailed explanation:
--------------------------------
I implemented a negative feedback via non-inverting input of OPAMP, and the voltages on OPAMP inputs (points A and B) differ by more than 500 mV. AFAIK, both points A and B should be about 12.5V, and the difference shouldn't be more than a few mV (at worst few dozen mV - maximum input offset voltage). What I measure is 12.7V at point A, but 13.4V at B!?
I thought maybe it was faulty chip (uA 741), so I tested with another one, even tried with other type of OPAMPs (NE 5532 and LM 358) - the large difference between inputs was still there. One other strange thing: when I connected a few more MOSFETs in parallel with the one shown here, the difference of input voltages changed with every MOSFET I added?
One final remark: in attempt to debug the problem, I reduced the circuit to the one shown here (what I actually tried to do was a power supply), and the behavior I just described pertains to this simple circuit.
Is someone has an idea why the voltages at points A and B differ so much, I'd love to hear it. Thanks!