engrMunna
Advanced Member level 4
- Joined
- Oct 25, 2010
- Messages
- 106
- Helped
- 6
- Reputation
- 12
- Reaction score
- 5
- Trophy points
- 1,298
- Activity points
- 2,071
Should we not compute only the first coefficient in IFFT in OFDM?
Hi,
I am editing this post because I think the previous one was quite confusing....Let me put my question in a more efficient way:
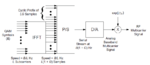
In OFDM Transmitter, when you do the IFFT of input samples x(0),x(1),x(2)....x(N-1), then at the output of the IFFT block you get a sequence \[\bar{X}\][0], \[\bar{X}\][1], \[\bar{X}\][2]..... \[\bar{X}\][N-1]. My question is, that do we then transmit \[\bar{X}\][0], \[\bar{X}\][1], \[\bar{X}\][2]..... \[\bar{X}\][N-1] one by one over the channel?
If that is so, don't you think we only need to transmit only one element from the set { \[\bar{X}\][0], \[\bar{X}\][1], \[\bar{X}\][2]..... \[\bar{X}\][N-1] } ??? because if you consider, lets say, \[\bar{X}\][0] then this particular element has information about all the samples of x(0),x(1),x(2)....x(N-1) (according to the formula of DFT) and we need only send only this element and not the complete set { \[\bar{X}\][0], \[\bar{X}\][1], \[\bar{X}\][2]..... \[\bar{X}\][N-1] }
Hi,
I am editing this post because I think the previous one was quite confusing....Let me put my question in a more efficient way:
In OFDM Transmitter, when you do the IFFT of input samples x(0),x(1),x(2)....x(N-1), then at the output of the IFFT block you get a sequence \[\bar{X}\][0], \[\bar{X}\][1], \[\bar{X}\][2]..... \[\bar{X}\][N-1]. My question is, that do we then transmit \[\bar{X}\][0], \[\bar{X}\][1], \[\bar{X}\][2]..... \[\bar{X}\][N-1] one by one over the channel?
If that is so, don't you think we only need to transmit only one element from the set { \[\bar{X}\][0], \[\bar{X}\][1], \[\bar{X}\][2]..... \[\bar{X}\][N-1] } ??? because if you consider, lets say, \[\bar{X}\][0] then this particular element has information about all the samples of x(0),x(1),x(2)....x(N-1) (according to the formula of DFT) and we need only send only this element and not the complete set { \[\bar{X}\][0], \[\bar{X}\][1], \[\bar{X}\][2]..... \[\bar{X}\][N-1] }
Last edited:
