yuvalkesi
Member level 5
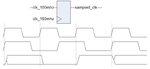
Suppose I want to sample low clock freq. (100MHz) signal with a high clock freq. (150MHz). Both siganl are produced at very close freq., only 50MHz difference.
Is the nyquist sampling rate valid here?
I mean, nyquist speaks about sampling an analog signal to a digital one, so when vice versa, the analog signal will be equal to the original. This is not the case, but still, it seems that a regular 2-flops synchronizer will not be suffice, so what is?
What is your opinion?
Thx.
Is the nyquist sampling rate valid here?
I mean, nyquist speaks about sampling an analog signal to a digital one, so when vice versa, the analog signal will be equal to the original. This is not the case, but still, it seems that a regular 2-flops synchronizer will not be suffice, so what is?
What is your opinion?
Thx.