yefj
Advanced Member level 4
Hello,I am trying to understand mathematicky why convolving with a window function makes spectral leakage smaller?
its not a magic thing, our data tone can be anywhere why mathematckly the convolution helps wit spectral leakage?
Thanks.
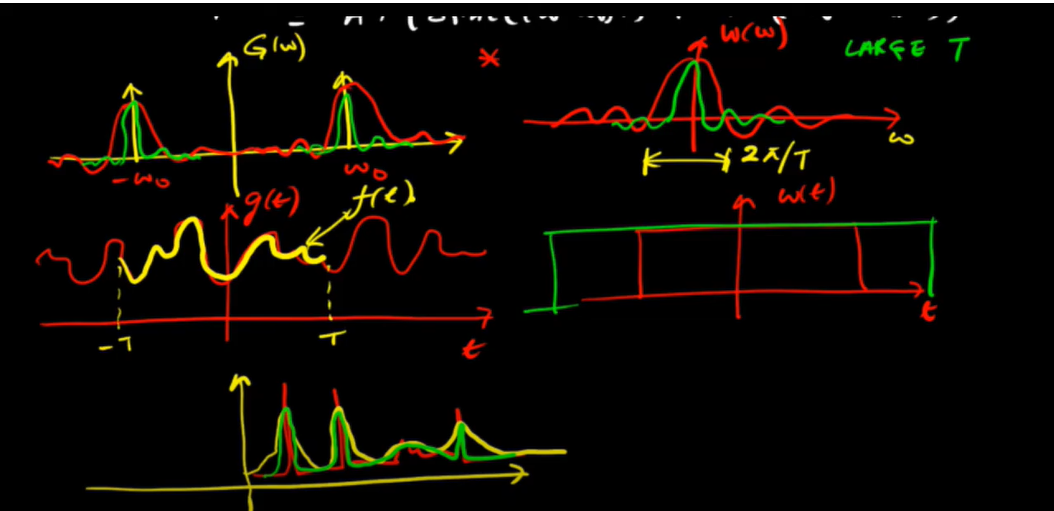
its not a magic thing, our data tone can be anywhere why mathematckly the convolution helps wit spectral leakage?
Thanks.