olemariendal
Newbie level 5

Hi,
I need help to determine the transfer function for a Sallen-Key low pass filter. I need help step by step for the mathematics steps for the transfer function.
The circuit is this:
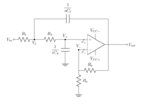
The steps i already have and end up with, is this.
\[\begin{equation}
V_{out}\cdot \left(\dfrac{\left(G_3+sC_4\right)\left(G_1+sC_2+G_3\right)}{G_3}\cdot (k-G_3)\cdot (k-sC_2)\right)=G_1\cdot (V_{in})
\end{equation} \]
\[
\begin{equation}
V_{out}=\dfrac{G_1\cdot (V_{in})}{\left(\dfrac{\left(G_3+sC_4\right)\left(G_1+sC_2+G_3\right)}{G_3}\cdot (k-G_3)\cdot (k-sC_2)\right)}
\end{equation}
\]
And then is \[G_{1,3}=\frac{1}{R_{1,3}}\]
\[\begin{equation}
V_{out}=\dfrac{\dfrac{1}{R_1}\cdot (V_{in})}{\left(\dfrac{\left(\dfrac{1}{R_3}+sC_4\right)\left(\dfrac{1}{R_1}+sC_2+\dfrac{1}{R_3}\right)}{\dfrac{1}{R_3}}\cdot (k)-\dfrac{1}{R_3}\cdot (k-sC_2)\right)}
\end{equation}\]
I'm stock here, please help me to continue, without CAS tools.
I know that the solution should be:
\[\begin{equation}
\dfrac{V_{out}}{V_{in}}=\dfrac{k}{s^2\cdot (R_1)\cdot (R_2)\cdot (C_2)\cdot (C_4+s)\cdot \left(R1\cdot (C2+R_3)\cdot (C_4+R_1)\cdot (C_4-k)\cdot (R1)\cdot (C2)\right)+1}
\end{equation}\]
Thanks for your time.
Sorry about me English writing skills.
I need help to determine the transfer function for a Sallen-Key low pass filter. I need help step by step for the mathematics steps for the transfer function.
The circuit is this:

The steps i already have and end up with, is this.
\[\begin{equation}
V_{out}\cdot \left(\dfrac{\left(G_3+sC_4\right)\left(G_1+sC_2+G_3\right)}{G_3}\cdot (k-G_3)\cdot (k-sC_2)\right)=G_1\cdot (V_{in})
\end{equation} \]
\[
\begin{equation}
V_{out}=\dfrac{G_1\cdot (V_{in})}{\left(\dfrac{\left(G_3+sC_4\right)\left(G_1+sC_2+G_3\right)}{G_3}\cdot (k-G_3)\cdot (k-sC_2)\right)}
\end{equation}
\]
And then is \[G_{1,3}=\frac{1}{R_{1,3}}\]
\[\begin{equation}
V_{out}=\dfrac{\dfrac{1}{R_1}\cdot (V_{in})}{\left(\dfrac{\left(\dfrac{1}{R_3}+sC_4\right)\left(\dfrac{1}{R_1}+sC_2+\dfrac{1}{R_3}\right)}{\dfrac{1}{R_3}}\cdot (k)-\dfrac{1}{R_3}\cdot (k-sC_2)\right)}
\end{equation}\]
I'm stock here, please help me to continue, without CAS tools.
I know that the solution should be:
\[\begin{equation}
\dfrac{V_{out}}{V_{in}}=\dfrac{k}{s^2\cdot (R_1)\cdot (R_2)\cdot (C_2)\cdot (C_4+s)\cdot \left(R1\cdot (C2+R_3)\cdot (C_4+R_1)\cdot (C_4-k)\cdot (R1)\cdot (C2)\right)+1}
\end{equation}\]
Thanks for your time.
Sorry about me English writing skills.


