low pass filter expression

[julian403]

For a low-pass filter:



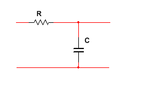
\[\frac{1}{1 + j 2 \pi fCR}\]

But some book gives the following expression

\[ \frac{1}{1 + j \frac{f}{fc} }\]

Where fc it's the cutoff frequency.

if C[F] * R[Ω] = and \[fc = [{s}^{-1}] \]

What happends with \[2 \pi\]?

Because for me it would be

\[ \frac{1}{1 + j \frac{2 \pi f}{fc} }\]

 

[Audioguru]

1 divided by 2 pi is very close to 0.16 so I calculate 0.16 divided by RC to find the cutoff frequency.

 

[Dominik Przyborowski]

Everything is OK. The ratio of two frequencies is equal to ratio of corresponding two angular frequencies, so 2pi disappears from equation. But still the relation between cut off frequency and its angular frequency is bounded by 2pi factor.
\[\omega_c = \frac{1}{R C} = 2 \pi ~f_c\]
\[\frac{\omega}{\omega_c} = \frac{2 \pi ~ f}{2 \pi ~f_c} = \frac{f}{f_c}\]

 

[julian403]

For what you said, the cutoff frecuency is smaller in a ratio of 2 \[\pi\] that the frecuency gives by RC. It's OK?

 

[Dominik Przyborowski]

You have to distinguish frequency and angular frequency. RC is a time constant which is inverse angular frequency which in turn is equal frequency multipied by 2pi [radians]. In fact there are not the same physical quantities.
For example, in your LP filter let R=1kΩ, C=1nF, gives time constant \[\tau\]=RC=1µs which correspond to angular frequency \[\omega\]=1M rad/s which is related to frequency f=160kHz.

 

[julian403]

Dominik Przyborowski that's the matter. I do not understand why aquantity like RC which has second as unit. If the angular velocity is s ^ -1 but also the frequency . Why then 1/RC [ s ^ -1 ] refers to the angular velocity and not to frecuency? Is there a physic basis?

 

[Dominik Przyborowski]

Because life is complex ;-)
I don't remember the origin of that but it should be explained in textbooks

 

[LvW]

Dominik Przyborowski that's the matter. I do not understand why aquantity like RC which has second as unit. If the angular velocity is s ^ -1 but also the frequency . Why then 1/RC [ s ^ -1 ] refers to the angular velocity and not to frecuency? Is there a physic basis?

Yes - because the capacitive impedance is 1/jwC and not 1/jfC. The background is the start of the calculation based on sin(wt).
This results in the lowpass function 1/(1+jwRC)