kviksand81
Newbie level 5

- Joined
- Jan 6, 2013
- Messages
- 8
- Helped
- 5
- Reputation
- 10
- Reaction score
- 4
- Trophy points
- 1,283
- Activity points
- 1,356
Hi there!
I have an assignment that goes as follows:
Pulse compression by using a Linear FM signal
1) Consider a (real) Linear FM signal with a center frequency, f0= 1250 MHz, a bandwidth, B = 100 MHz, and a length, T = 0.15 µs.
What puzzles me here is what to expect. In general, I would expect a linear compression of frequency to look like this in time:

But using an expression from the lecture material which is as follows (initial phase is omitted...):
\[\cos\left(2\pi\left(\frac{B }{2T }{\left(t-\frac{T }{2 }\right)}^{2 }\right)\]
Where "B" is the bandwidth of the pulse and "T" is the pulse duration, I get something that looks like this (which is seemingly correct, at least according to ESA):

Source: https://earth.esa.int/handbooks/asar/aux-files/ephimg-22242712.gif
Why is that? Is this due to something about the sampling of the signal or what is it? In this code I've only sampled the signal at 2 times fmax but I have been playing around a bit with the samplerate without getting much wiser.
The code I've written is following:
If I insert the carrier frequency in the expression as follows (initial phase is omitted...):
\[\cos\left(2\pi\left({f}_{c}\cdot {t}+\frac{B }{2T }{\left(t-\frac{T }{2 }\right)}^{2 }\right)\]
I get this:
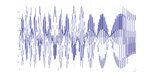
This does not at all look like what I would expect. Am I on the right or wrong track here? Any help, comments or clues is appreciated! I've spend quite a bit of time trying figuring this out but now I have to ask for a little bit of help!
Best Regards,
I have an assignment that goes as follows:
Pulse compression by using a Linear FM signal
1) Consider a (real) Linear FM signal with a center frequency, f0= 1250 MHz, a bandwidth, B = 100 MHz, and a length, T = 0.15 µs.
- What is the required sampling frequency, fs?
- Derive an expression for the pulse.
- Generate 1024 samples with the signal in MATLAB.
- Display the signal (time vs. magnitude). Display the spectrum (freq. vs. magnitude).
- Generate the same signal with a factor 8 over-sampling. Observe the difference
between the appearance of the signal without and with over sampling. Does the latter
provide more information for a computer? Does it provide more information for a
human?
between the appearance of the signal without and with over sampling. Does the latter
provide more information for a computer? Does it provide more information for a
human?
- Display the signal (time vs. magnitude). Display the spectrum (freq. vs. magnitude).
What puzzles me here is what to expect. In general, I would expect a linear compression of frequency to look like this in time:

But using an expression from the lecture material which is as follows (initial phase is omitted...):
\[\cos\left(2\pi\left(\frac{B }{2T }{\left(t-\frac{T }{2 }\right)}^{2 }\right)\]
Where "B" is the bandwidth of the pulse and "T" is the pulse duration, I get something that looks like this (which is seemingly correct, at least according to ESA):

Source: https://earth.esa.int/handbooks/asar/aux-files/ephimg-22242712.gif
Why is that? Is this due to something about the sampling of the signal or what is it? In this code I've only sampled the signal at 2 times fmax but I have been playing around a bit with the samplerate without getting much wiser.
The code I've written is following:
Code:
clear, close all;
fc = 1250*10^6; %Carrier frequency
BW = 100*10^6; %Bandwidth
fh = fc+(BW/2); %Highest frequency component
fs = 2*fh; %Nyqvist sample rate
Tpulse = 150*10^-9; %Pulse duration
Tstep = 1/fs; %Time-step resolution of input signal
t = [0:Tstep:Tpulse]; %Time vector generation
y = cos(2*pi*(BW/(2*Tpulse)*(t-(Tpulse/2)).^2));
plot(t,y);If I insert the carrier frequency in the expression as follows (initial phase is omitted...):
\[\cos\left(2\pi\left({f}_{c}\cdot {t}+\frac{B }{2T }{\left(t-\frac{T }{2 }\right)}^{2 }\right)\]
I get this:

Code:
clear, close all;
fc = 1250*10^6; %Carrier frequency
BW = 100*10^6; %Bandwidth
fh = fc+(BW/2); %Highest frequency component
fs = 2*fh; %Nyqvist sample rate
Tpulse = 150*10^-9; %Pulse duration
Tstep = 1/fs; %Time-step resolution of input signal
t = [0:Tstep:Tpulse]; %Time vector generation
y = cos(2*pi*(fc*t+BW/(2*Tpulse)*(t-(Tpulse/2)).^2));
plot(t,y);This does not at all look like what I would expect. Am I on the right or wrong track here? Any help, comments or clues is appreciated! I've spend quite a bit of time trying figuring this out but now I have to ask for a little bit of help!
Best Regards,
Last edited:
