mskh744
Newbie level 5
Hello everyone,
I have a circuit that produce an impulse response function of an RC filter, it looks like this:
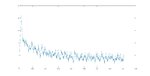
Theoretically, the impulse response in time domain is equivalent to the transfer function in the frequency domain. I have two vectors 'x' and 'y' imported from the circuit simulator where x is a time axis and y is the impulse response function of the filter.
I need to evaluate this response and see how accurate it is in describing the filter poles and zeros. The purpose is measuring the impedance of this filter by cross correlating a white noise stimulus with its response. The cross correlation function (CCF) is supposed to be identical to the impulse response and hence if analyzed I can quantify this filter ch's.
How can I get the exact (or very close approximation) value of total parallel R and C of the filter from this curve so I compare it to my filter values and evaluate this process?
I tried getting the fft of the impulse response and plotting the real and imaginary vs frequency but I get curves that I don't understand. Here's the Matlab code I wrote to generate the following plots.
The 3 plots generated looks like this :


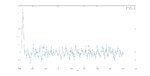
I can't decode any information from these curves about the RC filter. The filter I used to generate that CCF has a total parallel R of 50KOhm and total parallel C of 300pF. Any chance of retrieving that information? maybe I'm missing some normalization factor somewhere. The Nyquist plot doesn't make any sense to me as well as the mag and phase curves. I would appreciate your help to solve this issue.
I have a circuit that produce an impulse response function of an RC filter, it looks like this:

Theoretically, the impulse response in time domain is equivalent to the transfer function in the frequency domain. I have two vectors 'x' and 'y' imported from the circuit simulator where x is a time axis and y is the impulse response function of the filter.
I need to evaluate this response and see how accurate it is in describing the filter poles and zeros. The purpose is measuring the impedance of this filter by cross correlating a white noise stimulus with its response. The cross correlation function (CCF) is supposed to be identical to the impulse response and hence if analyzed I can quantify this filter ch's.
How can I get the exact (or very close approximation) value of total parallel R and C of the filter from this curve so I compare it to my filter values and evaluate this process?
I tried getting the fft of the impulse response and plotting the real and imaginary vs frequency but I get curves that I don't understand. Here's the Matlab code I wrote to generate the following plots.
Code:
x=x-0.0397; %shift for x axis (I neglect the first CC cycle as the system wouldn't have reached steady state yet)
yy1 = smooth(x,y,0.03,'loess'); % smoothing the curve to get better readability later. I'm aware this affects the total realized impedance.
figure
plot(x,y,x,yy1,'--')
legend('CCF','filtered CCF')
xlabel('time')
ylabel('V')
n=length(yy1);
z=fft(yy1)/n;
fs=10e3;
f=fs/2*linspace(0,1,n/2+1);
z=z(1:n/2+1);
R=real(z);
i=imag(z);
mag=abs(z);
phase=angle(z);
figure
plot(R,i)
ylabel('Imaginary');
xlabel('Real')
legend('Nyquist plot')
figure
subplot(2,1,1)
semilogx(f,mag)
legend('Magnitude')
xlabel('f')
ylabel('mag')
subplot(2,1,2)
semilogx(f,phase)
legend('Phase')
xlabel('f')
ylabel('degree')The 3 plots generated looks like this :



I can't decode any information from these curves about the RC filter. The filter I used to generate that CCF has a total parallel R of 50KOhm and total parallel C of 300pF. Any chance of retrieving that information? maybe I'm missing some normalization factor somewhere. The Nyquist plot doesn't make any sense to me as well as the mag and phase curves. I would appreciate your help to solve this issue.