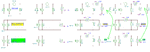how to nortonize this?

[PG1995]

Hi

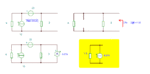
Please have a see on the following link: https://img339.imageshack.us/img339/3438/imgmw.jpg

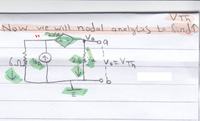
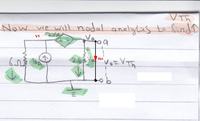
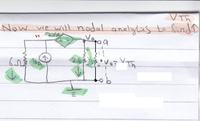
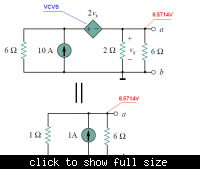
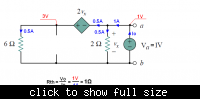
You also see my question there. There would be potential drop for Vo. I have also read that when the loop is traversed in the direction of loop current, then the IR term is subtracted; if the loop is traversed in the direction opposite to the direction of current, then IR term is added. Please help me. Thanks.

 

[mister_rf]

For the Nortonized circuit

R_eq= (R1R2)/(R1+R2)= 1.5 ohms

R1=2 ohms
R2=6 ohms

I_eq= I -(2V_x )/R2

also if
V_x= I_eq*R_eq
we obtain

V_x= (R1R2I)/(3R1 +R2)= 10V
I_eq= 10- (20/6)= 40/6=6.6(6)A


:-D

How To Nortonize a Given Circuit? ~ electricalstechnology

 

[PG1995]

Thanks a lot, Mr. RF! :grin:

 

[KerimF]

I am afraid that the answer is:
I_norton = 10A
R_norton = 1 ohm

To find I_norton, we made a short (it is like placing a resistor of zero ohm) between terminals (a) and (b).
The current in this short is I_norton.
In this case, Vx=0 hence the dependent source 2Vx is also zero.
Therefore the source current (10A) will find its easiest path at the shorted branch only (no current will flow in the resistors 6 ohms and 2 ohms).
In other words:
I_norton = 10 A

To find R_norton, we do as you did
Let us write the equations.
Loop1:
I1*6 - 2*Vx + (I1-I2)*2 = 0 [equation 1]
Loop2:
(I2-I1)*2 - Vo = 0
-2*I1 + 2*I2 = Vo [equation 2]
But
Vx = Vo [equation 3]
Replacing Vx in [equation 1]:
I1*6 - 2*Vo + (I1-I2)*2 = 0
I1*6 + I1*2 - I2*2 = 2*Vo
8*I1 - 2*I2 = 2*Vo [equation 4]
Adding [equation 4] and [equation 2]:
6*I1 = 3*Vo
2*I1 = Vo [equation 5]
Replacing 2*I1 of [equation 5] in [equation 2]:
-Vo + 2*I2 = Vo
2*I2 = Vo + Vo
I2 = Vo [equation 6]
On this circuit:
R_norton = Vo / I2 = Vo / Vo = 1 ohm

 

[mister_rf]

Let's test the circuits:
:grin:

That's the error you have made:

In this case, Vx=0 hence the dependent source 2Vx is also zero.

 

[jony130]

Bat when you dealing with dependent sources you can not short the dependent sources when you want to find Rth.
So first we want to find Vth

So have one KCL equation
10A = V1/6Ω + Vo/2Ω

And additional KVL equation

V1 = Vo + 2*Vo


then we solve for Vth

10A = (Vo + 2Vo)/6Ω + Vo/2Ω

Vo = Vth = 10V

Now we need to find the Isc current that is flowing from a to b when a & b are shorted together



We clearly see that Vx=0; and Isc = 10A

So Rth = 10V/10A = 1A

Int = 10V/1Ω = 10A

So the finally solution is Inorton = 10A ; Rth =1Ω

---------- Post added at 11:31 ---------- Previous post was at 11:19 ----------

mister_rf your simulation are wrong, you must use VCVC
If we connect 6Ω to A and b terminals to the original circuit

We can find Vo
10A = V1/6Ω + Vo/2Ω+Vo/6Ω
V1 = Vo + 2*Vo
10A = (Vo + 2*Vo)/6Ω + Vo/2Ω+Vo/6Ω

Vo = 60/7 = 8.57142857142857142857V

And for RL = 2Ω
Vo = 20/3 = 6.666V

 

[mister_rf]

Bat when you dealing with dependent sources you can not short the dependent sources when you want to find Rth.

Why? :grin:
Normally you remove all voltage sources but retain their internal resistances, if any... So, in this case, what's the internal resistance of the dependent sources ?

 

[KerimF]

Let's test the circuits: :grin:
That's the error you have made:

I wonder if we are taking about the same circuit.
I think you agree that to find I_norton (or Ish), we do a short at the terminals of interest ( as a and b ). It happens that Vx is the potential of Vb-Va which is now 0V, so in this particular case, the dependent voltage source has 2*Vx = 0 too as its voltage.

About removing or not a depedent source when finding R_norton (that is Rth) may not be obvious. So as we know, to find Rth we usually add a source (say a voltage source as Vo) at the terminal then we find out Vo/I(Vo) after removing the effect of the other sources in the circuit (voltage and current). Since here we are not sure about the dependent sources, I kept all sources and analysed the circuit as it shown on the 4th circuit (at the bottom on "Norton_03.pdf" attached). It has the last word I guess, to me in the least.

IMPORTANT:
The good news is that ALWAYS:
R_th = R_norton = V_th / I_norton

 

[jony130]

Why?
Normally you remove all voltage sources but retain their internal resistances, if any...

Yes, but only if the network has no dependent sources, we turn off all independent
sources.

If the network has dependent sources, we turn off all independent
sources and dependent sources are not to be turned off because they are controlled by circuit variables.
Basic electric circuit theory: a one ... - Google Ksi
Simply change in your simulation the 20V independent source to dependent sources VCVS (voltage-controlled voltage-source).
And you will see your error.
Or simply find Vo for this circuit:

So, in this case, what's the internal resistance of the dependent sources ?

For our case Rth = 1Ω = internal resistance of this circuit

 

[mister_rf]

I wonder if we are taking about the same circuit

:grin:
Yes, you are right, mea culpa.
I was thinking like a fixed condition for Vx, instead of a time variable function….
Back to the drawing board.

 

[_Eduardo_]

Why? :grin:
Normally you remove all voltage sources but retain their internal resistances, if any... So, in this case, what's the internal resistance of the dependent sources ?

Because the value of a dependent source depends of the unknowns.

These are properties of linear systems. if you have a matrix expression:

AE1 + BE2 = X + CE3 .... ; Ex: voltage sources
​

the solution can be expressed as the sum of:

X1 = AE1
X2 = BE2
X3 = CE3
....
X = X1 + X2 + X3 + ...
​

But if any of the Ex is a dependent source, its value depends of X, and therefore the expression is no longer valid.

 

[KerimF]

This is what I am always afraid to happen to me... that is to miss something obvious after solving the tough problems of a project. The bad news is that I can't avoid doing silly mistakes in hardware and software. The good news, I end up correcting them... to do other ones :grin:

 

[PG1995]

Hi everyone,

Sorry, I didn't read any of the posts except post #2 by Mr. RF. I have solved the problem. You can have a look if you like:
Part 1: https://img5.imageshack.us/img5/6241/part1dp.jpg
Part 2: **broken link removed**

Regards
PG