Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
Here is the problem: View attachment 105388.
For the 1st one, It's the low pass filter config. However, I think it's not possible to tell so just based on the Input and Output Voltage graph.
2nd one, i actually have no clue.
3rd question, would the Probe be placed on the left hand side of the resistor?
Thank you.
I don't agree with the comment. The response to a step function contains all information about a linear circuit. For the present square wave case, an additional assumptions must be made to make it equivalent to a step function: All circuit time constants are sufficiently short compared to the square wave period. Apparently this is the case.
The circuit doesn't act as an integrator (would involve a pole at frequency zero, respectively long time constant). It's exactly a first order low pass, it's time constant is lower than 1/10 of the square wave period. The nature of the circuit can be clearly seen from the exponential response in time domain.
Fourier analysis shows that the triangle wave is created by adding the even harmonics
afaik triangle is created with odd harmonics. with alternating sign, and with squared attenuation.
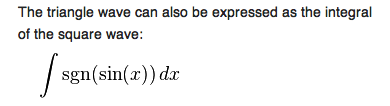
btw.
Filtering (in the meaning of lowpass, highpas...) will never add any frequencies. but it can attenuate or amplify the given amplitudes of the existing frequencies.
From my experience:
I find it hard to analyse the signals frequency components just by a view of a graph. It looks so different when a phase shift is added to the frequency components.
Klaus
I fully agree with that.Nevertheless I found it has this statement, regarding a triangle wave being the integral of a square wave.
The Falstad fourier series applet is quite instructive in visualizing the harmonic composition of common waveforms.
https://www.falstad.com/fourier/
Take a perfect squarewave that has no even harmonics and filter it with an 8th-order switched capacitor Butterworth lowpass filter like I have done. The output is a good sinewave with very low distortion. The output also has no even harmonics.
Then make an over-sampled stepped "sine" waveform with 10 steps and filter it with the 8th-order filter like I have done. The output sinewave is so good and its distortion is so low that it is difficult to measure.

There is an attached picture to this. The sentence is corresponding, but the formula is only for a sine input and not a square wave.
There's the term 'sgn'. It's a roundabout way to obtain a square wave.