HFSS-ciruclar waveguide port field display

[guyvaisman]

Hello ,i'm new to hfss and this forum and i have a question that i hope will be answerd:
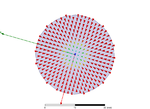
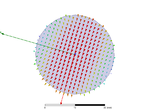
i'm trying to simulate a 20mm radius circular waveguide in hfss. i did a port solution only on the first 6 modes
and only the 3rd and the 6th mode made sense to me . that matched my analytical calculations concering the cut-off frequancies and the port field display matches the shape the electric field should be ( the 1st mode is a TM mode- the electric field is radial , and the 2nd one is a TE mode -the electric field is azimuthical).i've add the port field display images to make myself clear . it seems to me that i should be using only the 3rd and 6th modes. what am i doing wrong ?
thank alot !
guy .

 

[Azulykit]

You might find Moreno or Southworth helpful references for circular waveguide modes. The mode numbers in HFSS do not often match the numbering conventions in the literature. That adds fun to the effort.

 

[eraste]

Hi guyvaisman,

The fundamental mode of a circular waveguide is the TE11 mode and this mode is double degenerate ( in sinus and cosinus) so the first two modes on HFSS appear to be 90° rotated (mode 1 and mode 2 on your Thumbnails). After, you have TM01 mode that is non degenerate and has a circular symetry (mode 3 on your thumbnail). Then, follow, TE21 , double degenerate sin and cos (mode 4 and mode 5 on your thumbnail). and finally the three degenerate modes , TE01 , TM11 (x2 degenerate in sin and cos) (TE01 mode 6 of your thumbnail).

HFSS give the same exact list of the circular waguide mode than you can find in microwave book. Nethertheless, HFSS don't give the name but only classify the modes by increase cutoff frequencies and after numbered them.

That's all.

Good work in your HFSS simulations.

 

[guyvaisman]

Hello eraste,
thanks for the reply ,now i understand what are those other modes i got. what i still don't understand is why all those modes with sin and cos dependency propagate?
the structure is azimuthal symmetric so only TM0m and TE0m modes should exist.why am i wrong ?
thank alot ,
guy .

 

[eraste]

Hi,
The structure has a circular symetry but the modes have not all the circular symetry. In fact the tangential component of the electric field must be null on the waveguide wall. It means that the electric field has no component or has a normal component. The sin and cos dependence is an analytic solution of the Maxwell Equation. To be more accurate, the sin and cos are function of (m x Teta) in circular coordinate, so when m=0 the mode is no degenerate and is absolutly circular (no dependency of Teta). On the other side, when m is different of 0 the mode is degenerate (because sin and cos are present) but the symetry is not circular.
To conclude, these no circular modes (when m different of 0) exist and propagate too and have their own cutoff frequencies calculated from the zero of Bessel functions for the TM mode or zero of the derivate of Bessel functions for TE modes. They answer to the Maxwell Equations.

later.