bubulescu
Member level 3

- Joined
- Sep 10, 2009
- Messages
- 65
- Helped
- 12
- Reputation
- 24
- Reaction score
- 12
- Trophy points
- 1,288
- Activity points
- 1,897
Hello
I tried implementing this in LTspice, but I don't seem to get good results. I am using for this the IDCT/IDST, and here are the results for wc=pi/2, 21st order, between a normal un-windowed sinc filter, V(fir), and a FS, V(x):

and the coefficients:
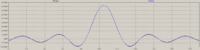
For this example in particular, I had to make them a type II, odd sampling (for FS), otherwise the differences would have been much bigger. This way, at least, I got the wc right.
Now, the question about this is must I make the IDCT on fixed, power of two number of samples or can I do it for x=0:M/2 ? I ask this because Octave gives a different answer, so I took a peak at its fir2.m and there it interpolates the frequency to the next power of two, then it does the IDFT and then it chooses every Mth point. But, the formula is a function of M, the order, at least as I can see it on Burrus' cnx.org collection: https://cnx.org/content/col10598/latest/ .
At any rate, the results so far seem to be the less attenuated versions of the "real" ones. Hopefully someone can shed some more light in this.
Anticipated thanks,
Vlad
I tried implementing this in LTspice, but I don't seem to get good results. I am using for this the IDCT/IDST, and here are the results for wc=pi/2, 21st order, between a normal un-windowed sinc filter, V(fir), and a FS, V(x):

and the coefficients:

For this example in particular, I had to make them a type II, odd sampling (for FS), otherwise the differences would have been much bigger. This way, at least, I got the wc right.
Now, the question about this is must I make the IDCT on fixed, power of two number of samples or can I do it for x=0:M/2 ? I ask this because Octave gives a different answer, so I took a peak at its fir2.m and there it interpolates the frequency to the next power of two, then it does the IDFT and then it chooses every Mth point. But, the formula is a function of M, the order, at least as I can see it on Burrus' cnx.org collection: https://cnx.org/content/col10598/latest/ .
At any rate, the results so far seem to be the less attenuated versions of the "real" ones. Hopefully someone can shed some more light in this.
Anticipated thanks,
Vlad