[SOLVED] Calculate an RC on-delay query about maths approach

[d123]

Hi,

Could some-one tell me if my maths reasoning is right or wrong here, please:

I want to turn on a BJT slightly after a logic output signal or a button is pressed. I'm assuming average button press by a human exceeds 2 milliseconds.

Maths theory (of mine to solve my problem) is following:

1 Tau = RC = ~63% Vsupply
5 Tau = 5RC = ~99% Vsupply

Vsupply is 3.9V to 6.6V
BJT base voltage turn-on is approx. 0.55V
R = 22k
C = e.g. 147nF

0.55V/3.9V = 0.141 Tau
0.55V/6.6V = 0.083 Tau

22k * 147nF = 1 Tau = 0.00323s
So, 5 Tau = 0.01617s
0.01617s * 0.083 Tau = 0.00134s to reach 0.55V at 6.6 Vsupply
0.01617s * 0.141 Tau = 0.00227s to reach 0.55V at 3.9 Vsupply

Is that method for the maths correct or not?

As can be seen from the schematic, original idea of one RC on an NPN base to achieve my goal didn't work, so I resorted to the 'randomly add more components and simulate over and over until it looks right' approach... I have no idea how to work out the time constants for the C2+R3 and C3+R4 networks yet as I haven't had time to think properly about what's happening there yet.

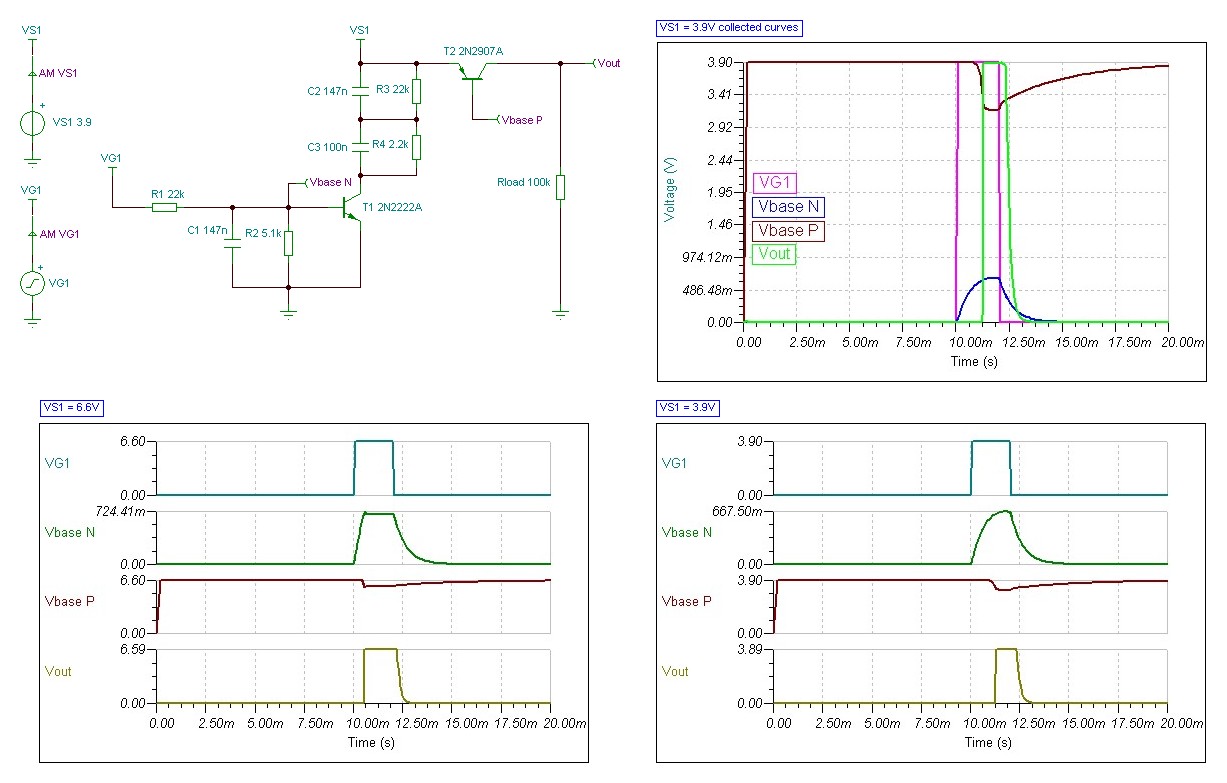
Anyway, is the NPN turn-on delay calculation method correct or incorrect, please?

Thanks

 

[std_match]

VbaseN = Vsupply * (1 - e^(-t/RC))
R = 22k, C = 147n, Vsupply = 3.9V, VbaseN = 0.55V gives t = 0.49 ms
R = 22k, C = 147n, Vsupply = 6.6V, VbaseN = 0.55V gives t = 0.28 ms

 

[FvM]

R2 must be factored in

\( V_{baseN} = V_{supply} \frac{R_2}{R_1+R_2}(1 - e^{-t\frac{R_1+R_2}{R_1R_2C}}) \)

Delay with 3.9 V increases e.g. to 0.84 ms

 

[std_match]

R2 must be factored in

\( V_{baseN} = V_{supply} \frac{R_2}{R_1+R_2}(1 - e^{-t\frac{R_1+R_2}{R_1R_2C}}) \)

Delay with 3.9 V increases e.g. to 0.84 ms

Correct! R2 was not used in the original calculation, and I didn't notice it in the schematic.

 

[KlausST]

Hi,

0.55V/3.9V = 0.141 Tau
0.55V/6.6V = 0.083 Tau

No, this is not tau. tau is a time constant with the unit "second"
0.55V / 3.9V = 0.141 = 14.1%

and 1 tau equals to 63% (or 37% = 0.37 error to full 100%)
(more exact: 0.36788. in the following I caclulate with the exact values, but show 2 digits only)
I like to do the math with the "error".
1 tau => 0.37^1 = 0.37 error => 1 - 0.37 = 0.63 = 63%
2 tau => 0.37^2 = 0.14 error => 1 - 0.14 = 0.86 = 86%
3 tau => 0.37^3 = 0.05 error => 1 - 0.05 = 0.95 = 95%
4 tau => 0.37^4 = 0.02 error => 1 - 0.02 = 0.98 = 98%
5 tau => 0.37^5 = 0.01 error => 1 - 0.01 = 0.99 = 99%

you may use a sheet of paper and a pencil to draw the curve. it starts at 0 tau with 0%

so now you neet to calculate how many tau 0.141 means. This is an error of 1-0.141 = 0.859
x = log(0.859) / log(0.37) = 0.153
this means the voltage rise from 0V to 0.55V (related to 3.9V) takes 0.153 tau

now R x C = tau = 22k x 147n = 3.23ms
then 0.153 tau = 0.153 x 3.23ms = 495us
(the same as std_match calculates more elegantely...and I also did just use the values from your text, without validating them :-( )

Klaus

 

[Akanimo]

R2 must be factored in

\( V_{baseN} = V_{supply} \frac{R_2}{R_1+R_2}(1 - e^{-t\frac{R_1+R_2}{R_1R_2C}}) \)

Delay with 3.9 V increases e.g. to 0.84 ms

Hi,

This is a good catch. However, I believe the calculation is even more involved as the base-emitter junction, just like R2, will also be conducting current while C1 is being charged.

I believe a MOSFET instead of a BJT would make the calculation easier.

 

[FvM]

This is a good catch. However, I believe the calculation is even more involved as the base-emitter junction, just like R2, will also be conducting current while C1 is being charged.

I wanted to show a correct calculation for the linear part of the differential equation, not solve it for the complete circuit. As longs as Ib << I(R2), the base current can be ignored for the Vbase calculation. That's effectively the case for the given circuit dimensioning.

The overall delay is affected by PVT variations (process = transistor parameter tolerances, V = supply voltage, T = temperature), it doesn't make much sense to calculate the behavior of an inherently unexact circuit exactly.

 

[d123]

Hi,

Thanks for corrections about incorrect maths and for providing the correct formulas, very helpful.

I understand one formula, the log()/log() one, but the other has two terms I'm unsure of:

What is 'e' here? 2.71828 or the desired voltage of 0.55V?
What is '-t' here? Desired delay time? Why is it negative?

Thanks.

 

[Akanimo]

Hi,
...
What is 'e' here? 2.71828 or the desired voltage of 0.55V?
...

2.71828

...
What is '-t' here? Desired delay time?
...

Yes. In your design t = 2 ms like you explained initially.

...
Why is it negative?
...

t is not negative. It's just indices. e^-(t/tau) = 1/e^(t/tau)

 

[FvM]

Read about RC circuit step response, e.g.: https://en.wikipedia.org/wiki/RC_circuit#Time-domain_considerations

 

[Akanimo]

Breaking down into easier steps,

\( V_{sig} = V_{supply}\frac{R_2}{R_1 + R_2}\)

\( x = ln\frac{V_{sig}}{V_{sig} - V_{baseN}}\)

\( C = \frac{(R_1 + R_2)t}{R_1R_2x}\)
Where t = delay time

From here, \( R_1\) and \(R_2\) could be selected based on desired base current to solve for C.

 

[d123]

Hi,

Thanks,

This is all very helpful, I was able to select a 4.7uF for the 22k NPN base - by calculating it, thanks to all yout explanations of both formulas - to get around 10ms off-delay (8ms and 15ms across supply range, from memory).