Mustaine
Member level 1
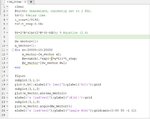
hello my friends currently i am studying the Problem-based learning communication Systems Using Matlab and Simulink by kwonge choi and huaping lıu.
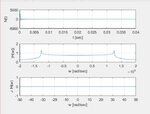
First i transformed the sinc function i'm expecting to see a square function but the function i get is so much different than the square one but when i applied a dely to the sinc transformed function becomes square. Can you explain why is that
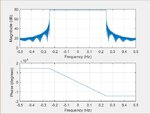
Also I'm having a problem about the bandwidth of the sinc function. When i transform the sinc function below i'm expecting to see a square wave which has a B bandwidth but no, the bandwidth is much bigger than B. Can you explain why is that. thanks
First i transformed the sinc function i'm expecting to see a square function but the function i get is so much different than the square one but when i applied a dely to the sinc transformed function becomes square. Can you explain why is that
Also I'm having a problem about the bandwidth of the sinc function. When i transform the sinc function below i'm expecting to see a square wave which has a B bandwidth but no, the bandwidth is much bigger than B. Can you explain why is that. thanks