Bandstop Elliptic Analog Filter Design

[ephraim13]

Hello everyone, i need your help about a problem listed below, i will be gratefull for your contributions.

Design a BSF with;

* Maximum Attenuation in passband region: 1dB (rippled)
* Minimum Attenuation in stopband region: 35dB (rippled)
* Stopband region: 2000>w>2500 (rad/sec)
*Passband region: 0-1300 and w>3600 (rad/sec)
* Maximum gain: 1

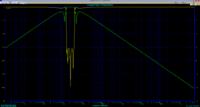
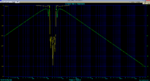
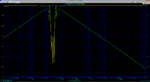
1-) Sketch the gain curve for obtained transfer function by using Matlab
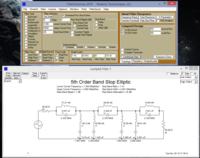
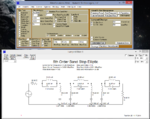
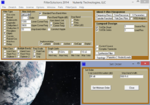
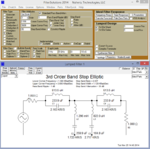
2-) Realize your transfer function as 1 Ohm lossless ladder network (LC)
3-) Realize your transfer function as multi-amplifier RC network
4-) Verify your network by SPICE (Obtain the gain curve and compare with the one obtained by MATLAB)
5-) Realize your transfer function as OTA-C network
6-) Verify designed passive circuit in the Laboratory (schematic required)

 

[crutschow]

Before we can help we need to know a lot more about what your knowledge level is:

What has your course instructor taught you about filters to this point?
Are you familiar with Matlab?
Do you know what a lossless ladder network is?
What Spice program are you using? Are you familiar with its use?
Do you know what an OTA-C network is?

 

[LvW]

As another question: Are you allowed to use one of the available filter design programs?
This would be a great help - at least for the first design step: Determination of the minimum filter order necessary to meet your specification.

 

[ephraim13]

I am familiar with Matlab and Nuhertz filter solutions but i cant be sure about the truth of the results.
I dont have much knowledge about OTA-C and Ladder networks, and dont know how to build them.

 

[LvW]

I am familiar with Matlab and Nuhertz filter solutions but i cant be sure about the truth of the results.
I dont have much knowledge about OTA-C and Ladder networks, and dont know how to build them.

You do not trust "Filter Solutions"? Why not? It`s pure mathematics!

 

[ephraim13]

I need someone to check my solution or compare the solutions of an expert. I dont have deep knowledge about filter design for that reason asking for a help who has an experience.

 

[FvM]

I need someone to check my solution or compare the solutions of an expert.

You didn't yet post any solutions to check.

 

[ephraim13]

- - - Updated - - -

Here are some of my results:
http://obrazki.elektroda.pl/5725434300_1416918367.png
http://obrazki.elektroda.pl/8962432800_1416918367.png
http://obrazki.elektroda.pl/6970930500_1416918368.png
http://obrazki.elektroda.pl/9570698500_1416918369.png
http://obrazki.elektroda.pl/7649285800_1416918370.png

 

[FvM]

Looks like a correct implementation of problem 2), impedance should be 1 instead of 50 ohm if understand the specification right.

 

[ephraim13]

Is the order Important? and also What kind of network is OTA-C?

 

[FvM]

Is the order Important?

Yes. You have used minimal order which seems an appropriate way.

and also What kind of network is OTA-C?

"operational transconductance amplifier" plus "capacitor". Did you ask Google for details?

 

[ephraim13]

Yes i searched for it but still dont know how to design it from transfer function. Is the 3rd order good approximation for this problem? And is my solutions correct for the relevant problems?

 

[FvM]

As far as I understand, you want the same filter characteristic for all implementations. So if the LC filter needs 5th order to implement, the active RC filters need it too.

Regarding OTA-C implementation, it's not supported by Nuhertz Filter Solution. But you can start with an active filter implementation based on second order building blocks ("Biquads") and replace it by an OTA-C biquad according to literature.

The fact that the exercise problem is given to you suggests that OTA-C has been already covered by your lectures?

 

[LvW]

Yes i searched for it but still dont know how to design it from transfer function. Is the 3rd order good approximation for this problem? And is my solutions correct for the relevant problems?

Just to avoid misunderstandings:
The program you have used (Filter Solutions from NuHertz) uses a somewhat uncommon method for specifying the filter order.
Normally, all bandpass and all bandstop filters have an even order only (corresponding to the number of poles). Hence, the lowest-order bandpass has the order n=2 - because it was derived from a first-order lowpass using the lowpass-bandpass transformation. This way of specifying the filter order is used in all other filter programs as well as all textbooks (to my knowledge).
In contrary to this method, the program "Filter Solutions" counts not the poles but the pole pairs. This is not false and all results are quite OK - however, one should know.
As a consequence, the last simulation as shown by you has three pole pairs (6 poles) and, hence, has the (classical) filter order n=6.

I have used another filter program (FilWiz) to find out the lowest filter order which meets your specification (I can specify damping requirements and the program calculates the filter order for different approximations) - and the result was:
Yes - based on an elliptical response, the filter order n=6 can fulfill your requirements (n=3 in Filter Solutions).

 

[FvM]

You are right, I assumed that Nuhertz had given 5 minimal order, but it's actually 3 (respectively 6 in usual filter metrics).

 

[ephraim13]

Thank so so much for your help and contributions. So, is the 3rd order approximation sufficient and accurate for my solutions? bcoz i have to verify in the laboratory with real circuit elements and show to same resultz on the oscilloscope.
Yes OTA-C is covered by my lectures but i dont know how re-design with them. Is there any other software that i can use for designing OTA-C

 

[ephraim13]

And the other issue that i faced while designing in Matlab: is this an IIR or FIR filter?

 

[LvW]

Thank so so much for your help and contributions. So, is the 3rd order approximation sufficient and accurate for my solutions? bcoz i have to verify in the laboratory with real circuit elements and show to same resultz on the oscilloscope.
Yes OTA-C is covered by my lectures but i dont know how re-design with them. Is there any other software that i can use for designing OTA-C

* 3rd order is not an "approximation"; it just gives the numer of pole pairs (in Filter Solution) and is identical to 6 poles (6th order) in "classical" terms.
* I do not know any program that incorprates OTA-C filters. But you should know that, in principle, several different hardware realizations (topologies) are possible:

(a) Series combination of several stages to be designed separately or (b) filter structures based on passive RLC reference filters (leapfrog synthesis).

* For my opinion, and with respect to your task No. 2 (your first post), this latter option is recommended.
(Hint: Leapfrog syntheseis simulates the state space equations of passive RLC filters using integrators only. These integrators can easily be realized in OTA-C technology. )

 

[andre_luis]

i have to verify in the laboratory with real circuit elements and show to same resultz on the oscilloscope

There is an option on Nuhertz for generate a SPICE model of the syntesized circuit so that you can perform an independent precise simulation before assemble circuit on real world.

 

[ephraim13]

Thank you so much for your contributions again