about twin-t filter parameter calculation

[lhlblue]

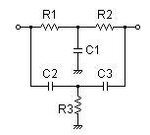
below is the schematic of twin-t filter, and the transfer function of it. in actual design, it can also be used for bandpass filter if connected between negative input and output of opamp. now, the twin-t network is a three order system, so, how to get the expression of center frequency f0 and quality factor Q? for two order system, we use 's^2+(2*pi*f0/Q)*s+(2*pi*f0)^2' to calculate f0 and Q, but for the three order system, how to calculate the parameter f0 and Q?
thanks all.

 

[godfreyl]

Assuming R1 = R2 = R, R3 = R/2, C2 = C3 = C, and C1 = 2*C,
then F0 = 1 / (2*pi*R*C)

My gut feel is that Q can't be easily be calculated (for a twin-t + opamp bandpass filter) as it depends entirely on the accuracy of the component values.

You could guarantee a certain minimum Q by using sufficiently close-tolerance components, but without measurement you wouldn't know how much better than the minimum it actually is.

Similarly, you could deliberately degrade the Q by mismatching components.

- - - Updated - - -

On the other hand, it's not totally unpredictable. According to Horowitz&Hill:

...a twin-T driven by a perfect voltage source is down 10dB at twice (or half) the notch frequency and 3dB at four times (or one-fourth) the notch frequency.

What component accuracy determines is the depth of the notch (and the response close to the notch frequency).

 

[LvW]

Hi Ihlblue,

The twin-T network is used as band stop (notch) filter for a particular selection of component values.
You get an ideal notch (neglecting tolerances) for
C1=C2+C3 and R3=R1||R2.

In this case you arrive at a second-order transfer function due to pole-zero cancellation.
Thus, you can apply the classical procedure to find the pole frequency and the pole Q.

 

[lhlblue]

ok, i know. but if the relationship C1=C2+C3 and R3=R1||R2 is not satisfied (there is mismatch), such as R1=R2=2*R3 and C2=C3=a*C1(a is not 1/2), so, how to get the expression of f0 and Q? or is there some simple expression here?
besides,

Similarly, you could deliberately degrade the Q by mismatching components.

, but what is the detailed relationship between Q degradation and mismatch (some examples?)?
thanks.

 

[LvW]

OK - here is a formula for the Q value (derived from G.S. Moschytz: Linear integrated networks):

Q=N/D
N=a(1-b)(1-c)
D=a^2(1-c)+(1-b)

with:
a=SQRT[RsCs/R3Cp] with Rs=R1+R2, Rp=R1||R2, Cp=C1+C2, Cs=C1C2/(C1+C2)
b=C2/(C1+C2)
c=R1/(R1+R2)

For ideal matched condition the Q value should be 0.5 (maximum value).
Good luck.

 

[FvM]

but what is the detailed relationship between Q degradation and mismatch (some examples?)?

Unless someone has already solved the problem, you can't seriously expect others do the calculation for you, I think.

Strictly speaking, Q is a parameter of the second order system and undefined for third order. Calculating parameter sensitivity of the ideal filter makes sense however. I'm sure, it can be derived analytically, but I also guess you won't want to do the calculation. Everybody is calculating sensitivities by numerical methods these days. You can do with a spread sheet calculator, by stepping parameters in a basic SPICE simulation, or using a tool like PSpice advanced analysis that does the calculation for you automatically.

 

[LvW]

Ihlblue,

with regard to FvM`s contribution (Q value) perhaps it is good to give the following explanation:
The Q expression in my last post is defined as the ratio center frequency-to-3dB bandwidth B.
B is the bandwidth measured for 3 dB attenuation.

 

[lhlblue]

LvW, as you said,

Q=N/D
N=a(1-b)(1-c)
D=a^2(1-c)+(1-b)

if C1=C2=2*C3(C1 and C3 inter-changed in my posted schematic), R1=R2=0.5*R3, then, a=1, b=c=0.5, so, Q=0.25, not 0.5.
besides, the Q expression does not include C3, but in my simulation, Q can be influenced by C3. am i wrong?
thanks.

 

[LvW]

if C1=C2=2*C3(C1 and C3 inter-changed in my posted schematic), R1=R2=0.5*R3, then, a=1, b=c=0.5, so, Q=0.25, not 0.5.
besides, the Q expression does not include C3, but in my simulation, Q can be influenced by C3. am i wrong?
thanks.

You are right. That means:
*Q=0.25 is correct.
*C3=C1+C2 (always).

Explanation: This restricting condition for C3 is called by the author: "potentially symmetric".
That`s all I can say.