Swend
Full Member level 4
- Joined
- May 14, 2019
- Messages
- 237
- Helped
- 10
- Reputation
- 20
- Reaction score
- 9
- Trophy points
- 18
- Location
- Roskilde, Denmark
- Activity points
- 2,304
As a service for the persons reading this post, I made the following calculations:
I took the first full pulse from the data file (SDS00001.CSV attached in previous thread) and it looks like this

Then I inverted the current by multiplying it with -1 and the result looks like this

Note that the current still goes negative while the voltage is positive.
Then I calculated instantaneous power P = U * I and energy ∫P

And I calculated the resistance R = U / I
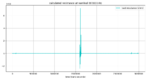
Note that the resistive spike occurs at the same time as the current crosses zero.
If I in fact have turned the CT the wrong way, then I would really have a "pertuum mobile" in my hands as the output energy would be 2.45J while input is 50mJ (calculated excluding losses i.e. the final amount of energy that enters "R") i.e. 4900% efficiency. So logic dictates that I could not have turned the CT the wrong way around, hence I still believe we are talking about true negative resistance.
In general, it may also be noteworthy that if the resistor "R" is disconnected from the source it behaves just like any ordinary resistor and has a resistance of 883K ohm.
I took the first full pulse from the data file (SDS00001.CSV attached in previous thread) and it looks like this

Then I inverted the current by multiplying it with -1 and the result looks like this

Note that the current still goes negative while the voltage is positive.
Then I calculated instantaneous power P = U * I and energy ∫P

And I calculated the resistance R = U / I

Note that the resistive spike occurs at the same time as the current crosses zero.
If I in fact have turned the CT the wrong way, then I would really have a "pertuum mobile" in my hands as the output energy would be 2.45J while input is 50mJ (calculated excluding losses i.e. the final amount of energy that enters "R") i.e. 4900% efficiency. So logic dictates that I could not have turned the CT the wrong way around, hence I still believe we are talking about true negative resistance.
In general, it may also be noteworthy that if the resistor "R" is disconnected from the source it behaves just like any ordinary resistor and has a resistance of 883K ohm.
Last edited: