Shady Ahmed
Member level 5
Hello, I am designing an integrator of a continuous time sigma delta ADC using a fully differential amplifier on cadence with input freq 1.5MHz and sampling freq at the comparator 256MHz.
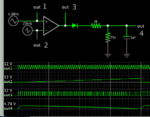
In the integrator we add resistance parallel to the cap to adjust the dc ,but it gives a dc gain (R2/R1) with a corner freq 1/(2(pi)R2*c) so what should be the range of the dc gain and the ratio between the corner freq and the i/p signal frequency to insure that it is operating in the integrating range after the corner frequency?
In the integrator we add resistance parallel to the cap to adjust the dc ,but it gives a dc gain (R2/R1) with a corner freq 1/(2(pi)R2*c) so what should be the range of the dc gain and the ratio between the corner freq and the i/p signal frequency to insure that it is operating in the integrating range after the corner frequency?