Junus2012
Advanced Member level 5

Dear friends,
The square low equations are very useful approximation but only applied to the strong inversion and not in advance short channel technology,
All the literature books, like Allen Holberg, Paul Gray, Behzad Rezavi, etc, are consedring the strong inversion in the design with VDS(sat) around 100 mV or more,
Until I start to read the books of David Benkley and Paul Jespers , ("Tradeoffs and Optimization in Analog CMOS Design" and "Systematic Design of analog CMOS Circuits),
The latter authors both assumes that minumum VDS(sat) for saturation voltage is above 200 mV as you kindly see from this image
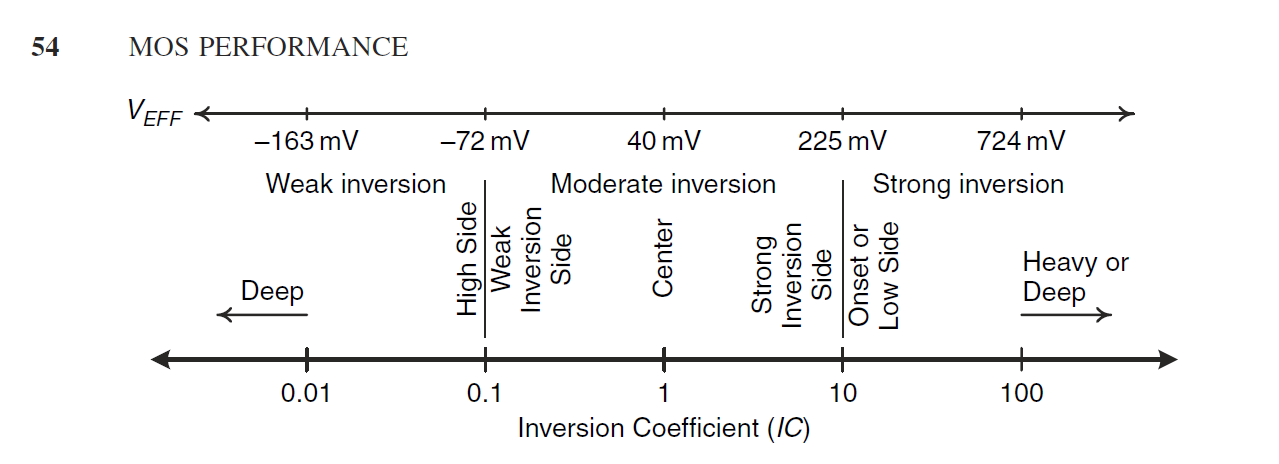
So my question, how the other books using the square low equations and they are not in the strong inversion, are they just approximating the solution as the 100 mV is at the border of strong inversion?
Bytheway, Gray stated that MOS enter the weak inversion if VDS(sat) is below 80 mV, which is quite different from the values given up
Thank you
Best Regards
The square low equations are very useful approximation but only applied to the strong inversion and not in advance short channel technology,
All the literature books, like Allen Holberg, Paul Gray, Behzad Rezavi, etc, are consedring the strong inversion in the design with VDS(sat) around 100 mV or more,
Until I start to read the books of David Benkley and Paul Jespers , ("Tradeoffs and Optimization in Analog CMOS Design" and "Systematic Design of analog CMOS Circuits),
The latter authors both assumes that minumum VDS(sat) for saturation voltage is above 200 mV as you kindly see from this image
So my question, how the other books using the square low equations and they are not in the strong inversion, are they just approximating the solution as the 100 mV is at the border of strong inversion?
Bytheway, Gray stated that MOS enter the weak inversion if VDS(sat) is below 80 mV, which is quite different from the values given up
Thank you
Best Regards


