How to plot a normalized TF

[netbug]

Dear all,

I am doing some Matlab code to simulate PLLs. I am using the book "PhaseLock Techniques" by Gardner. I wanted to replicate some of the graphs to check my understanding. However I can't.

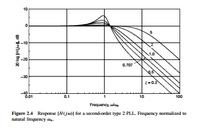
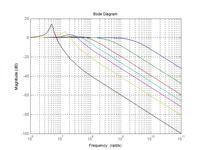
For eg. in the book Gardner plots 20 log|H(jw)| vs w/wn. Maybe this is a silly question, but all that I have in my TF are "symbolic variables", there are no defined values for each variable. As far as I know there is no way to generate a symbolic TF and apply a step to it.If somenone has the book, please refer to page 15 of the 3rd. edition.So there should be some known values to plot these curvesl ike, for instance, bandwidth. But then, this curves represent a particular case and not a generic one.

The TF used in the book is:

\[ H(s)=\frac{K(s+K/ 4\zeta^2)}{s^2 + Ks + K^2/4 \zeta^2}= \frac{K(s + 1/ \tau2)}{s^2 + Ks + K/ \tau2}\]

where
\[K=K_dK_oK_1= \frac{K_d K_o \tau2}{\tau1}\]

and

\[ \omega_n=\sqrt{\frac{K}{\tau2} }\] and \[ \zeta=\frac{1}{2} \sqrt{K \tau2}\]

and here you have a scanned image from Gardner's book:

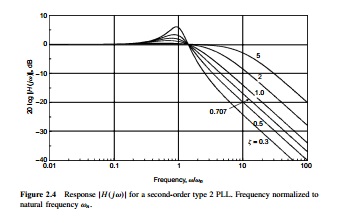
Now, how to plot mag(H(s)) vs w/wn and w/wK ? As \[ \tau2 \] and \[\tau1\] are time constants of the filter, we should know these values "a priori", correct ?

Thanks in advance.

Best regards,
Pedro

 

[LvW]

Hi netbug,

what is your problem?
The set of curves provided by F.M. Gardner shows some typical transfer function (second order) for some typical values of K and tau2.
These two parameters (K and tau2) solely determine the values for wn and Theta (remember: Pole Q=1/2*theta).
Of course, we have different natural frequencies wn - however, in case of normalization all curves meet in one single point.

 

[netbug]

Hi,

I am not still seeing the way it is done, I am sorry I know I am being dumb.

For eg. Are you suggesting that I should create a vector with tau2 points, and then generate K ? But K is affected by other gains and tau2 and tau1,as well. Do I have to care about that, or should I see K as one variable that can be sweeped ?

How would you do a simple function to do the same graph,as the one in the Gardner's book in Matlab ?

Cheers,
Pedro

 

[LvW]

Of course, K and tau2 are the only variables (independent on the fact that K is determined by some other parameters).
For example, start with a fixed K value and select suitable values for tau2 which lead to realistic damping values between e.g. 0.1 and 2.
Insert the values into the transfer function and plot the results.

 

[netbug]

Good afternoon,

I am sorry to post from the 3rd time. I did a small function in MatLab.

%% Plots magnitude of H(s)

K=5e7; %loop gain
zeta=[5 2 1 0.707 0.5 0.3 0.1]; %damping

for n=1:length(zeta)
tau2=((2*zeta).^2)./K;
wn=sqrt(K./tau2)
num=[0 K K./tau2];
den=[1 K K./tau2];
H_s=tf(num,den);
figure(3);
bodemag(H_s);
grid on;
grid minor;
hold on;
end
hold off;

But for different values of damping, we should have different values of gain. If this plot is done for several values of damping and always at the same frequency, so tau2 is always the same and wn as well. But this should not be true according to \[\omega_n = \sqrt{\frac{K}{\tau2}}\], once taking into account this formula fixing tau2 and zeta will give always the same loop gain, which I think it is not true, I thik that the gain varies with the damping.

So please HELP.

Cheers,
Pedro

 

[LvW]

Quote Pedro: "But for different values of damping, we should have different values of gain."

What means "we should" ? The situation is clear: The dc gain ALWAYS is unity (0 dB) since for s=0 we have the same expression in the numerator and the denominator (K^2/(2Theta)^2)

 

[netbug]

Hi,

I am not quite there yet, but I did some improvements, however the curves for different zeta values (damping), don't converge to the same point. There is no intersection.

I did what you wrote on the first post:
1 - I have chosen K (50e6)
2 - Found a value for tau2, such that zeta=0.707.
3 - Calculated the values for tau2=3.98e-8 and wn=3.55e-9

But then, maybe there is a mistake here. The first iteration I believe it is correct, but then I assume to have always the same filter, and then the same tau2, and I have calculated all the values for a fixed value of tau2 (maybe this is wrong because wn doesn't equal 1/tau2).

Regarding the normalization, do you divide every term by wn (numerator ad denominator) ?

Here is the MatLab code.
fo=40e6; % operating frequency
wo=2*pi*fo; % angular frequency
zeta=[5 2 1 0.707 0.5 0.3 0.1]; % damping
K=[2.52e9 4.10e8 1.10e8 5.02e7 2.52e7 9.10e6 1.05e6]; % Loop Gain

tau2=3.98e-8;
%zeta=1;
figure(3);
for n=1:length(zeta)
% tau2=((2*zeta).^2)./K;
wn=sqrt(K./tau2)

%num=[2*zeta*wn wn^2]
%den=[1 2*zeta*wn (wn)^2];
num=[2*zeta./wn 1]
den=[1./((wn)^2) 2*zeta./wn 1];
H_s=tf(num,den)

bodemag(H_s)
grid on;
hold on;
end
hold off;


and the figure


Thanks in advance.
Best regards,
Pedro

 

[LvW]

OK - I think the set of curves looks good and as expected, do you agree?

Quote: "Regarding the normalization, do you divide every term by wn (numerator ad denominator) ?"
No, of course not. Dividng each term by the sane number will not change the transfer function at all.
But it is your goal to normalize the curves regarding the pole frequency - that means: to keep the damping properties (Pole Q) and to have the same pole frequency.
For this purpose you need to analyze the transfer function for the normalized variable sn=s/wp.
Thus, for each single curve you must replace the Laplace variable s by sn*wp (wp being the corresponding pole frequency)

 

[netbug]

OK - I think the set of curves looks good and as expected, do you agree?

Thanks for having answered to one more question.
I think that the curves look ok, but I have used a concept that uses the time constant of the filter as being tau2, thus w3db=1/tau2 (let´s say the BW of the loop). And I am not sure that this is correct.
I agree with you that to obtain the Gardner's plot from my first post, every curve should have the pole on the same position. But this one is going to be tough, once changing the pole location, will change damping, etc .... I would really like to obtain that plot where all curves intersect on the same pole.

Regarding normalization, I am sorry to insist on this, for eg. tor normalize for w/K one should divide every term having "s"(jw) in the denominator by K, correct ?

Thanks for your patience.

Best regards,
Pedro

 

[LvW]

Regarding normalization, I am sorry to insist on this, for eg. tor normalize for w/K one should divide every term having "s"(jw) in the denominator by K, correct ?

No - it is not. I have answered this question of normalization before. You have to multiply the variable "s" with the particular value for the pole frequency.

 

[netbug]

Hi,

Understand your point. Please try to answer these questions point by point:

1 - If you have H=tf(num,den), where num=[4] and den=[2 3 4], the outcome will be (MatLab) 4/(2*s^2 + 3s + 4), the denominator is equivalent to:
\[\frac{2 \zeta \omega_n s + {\omega_n}^2}{s^2+2\zeta\omega_ns+{\omega_n}^2}\]
2 - As you said, we should have an sn=s*wp and Q=1/2 zeta to have the same damping properties for the pole. But what how do I calculate of the pole ?
3 - For a frequency of 40 MHz I took a decade from that, remaining 4 MHz and then I calculated the tau of the filter. Setting a value for C, using the impedance Z=1/sC I can discover the frequency of the pole. Is this approach correct ?
4 - I would like to normalize by K and by wn (w/wn and w/K), having the matlab notation in mind, as described in 1, how can I insert wn or K there ? I cannot multiply s by wp or K, the only way is to multiply all factors of the expression that are s, s^2, .... Thus, in expression 1 I should multiply 2 by wp and 3 by wp. Is this correct, so in summary I would obtain a plot mag(H(s)) vs w/wn or vs w/K.
5 - Please remember that, in the case, of w/wn what I want to obtain is
**broken link removed**

and not this
**broken link removed**

Thank you so much.

Best regards,
Pedro

 

[LvW]

3 - For a frequency of 40 MHz I took a decade from that, remaining 4 MHz and then I calculated the tau of the filter. Setting a value for C, using the impedance Z=1/sC I can discover the frequency of the pole. Is this approach correct ?
4 - I would like to normalize by K and by wn (w/wn and w/K), having the matlab notation in mind, as described in 1, how can I insert wn or K there ? I cannot multiply s by wp or K, the only way is to multiply all factors of the expression that are s, s^2, .... Thus, in expression 1 I should multiply 2 by wp and 3 by wp. Is this correct, so in summary I would obtain a plot mag(H(s)) vs w/wn or vs w/K.
5 - Please remember that, in the case, of w/wn what I want to obtain is
**broken link removed**
and not this
**broken link removed**

@3 - I don`t understand the meaning od the frequencies (4 and 40 MHz). In your expression, the pole frequency is wn (normally, it is called wp).
@4 - Why are you not able to use the variable "s" with a a fixed factor (a number)?
@5 - the attachements cannot be opened

 

[netbug]

I hope the plots are visible now

I would like to be able to plot something like this:


and not like this:



Best regards,
Pedro

 

[LvW]

"I would like to be able to plot something like this"...

OK - I have understood. That´s what you have stated already in post#7.
But why are you not able to normalize the functions with respect to wn?
For the different curves you have different damping and different wn values.
What is the problem if you insert a fixed factor wn to each "s" (NOT wp as mentioned in my post#8)?
(By the way - I have to correct my former statement that wn would be the pole frequency. Rather, it is the PLL natural frequency)

 

[netbug]

Hi,

New day, and the problems persist :-| .

I took the generic control function,

\[ H(s)= \frac{\omega_n^2}{s^2 + 2\zeta \omega_n s + \omega_n^2}\]

and derived for s=jw/wn so I obtained,

\[ H \left(j \frac{\omega}{\omega_n} \right)=\frac{\omega_n^2}{-\left(\frac{\omega}{\omega_n}\right)^2+ 2\zeta \omega + \omega_n^2} \]

And I believe, we have now, the normalized function.

So the question is, how to determine wn ?
1 - We can just ignore that this is a PLL (with a PI filter) and view it as a second order system. In this case \[ \omega_n =sqrt{K} \]. Later we can move a little further introducing the loop filter's TF. Do you agree ?
2 - For the case of the PLL presented with a PI Filter, \[ \omega_n=\sqrt{\frac{K}{\tau2}} \] and tau2 is the time constant of the filter which is proportional to w3db, correct ?
3 - Why there is an emphasys put on tau2 regarding tau1. That is, tau1 is almost forgotten. Is the integral path dominant over the proportional one ?

Best regards,
Pedro

 

[LvW]

......and derived for s=jw/wn so I obtained,

Pedro, why didn`t you follow my advice to MULTIPLY the variable "s" by a factor?

OK - I see it´s best to present a simple example:

H(s)=1/D(s) with denominator D(s)=1+0.1*s+0.01*s^2.

This is a transfer function with a corner frequency at wg=10 rad/sec. (equivalent to fg=10/6.28 Hz).
Now we want to normalize.
Thus, in the normalzed denominator Dn(s) the variable "s" is multiplied by the factor of "10" (That means: We want to have the normalized variable sn>>s/10 leading to s>>sn*10) .

Thus: Dn(s)=1 + 0.1*10*s + 0.01*10*10*s^2=1+s+s^2.

Plotting the normalized function Hn(s)=1/Dn(s) gives the normalized corner frequency wg,n=1 rad/sed (equivalent to fg,n=1/6.28 Hz).

I hope it`s clear now, OK?

 

[netbug]

Hi,

Thanks a lot for everything. The plots, now, look like they should.

Thanks for your precious help.

Best regards,
Pedro