sherif96
Member level 4

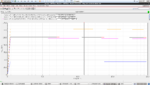
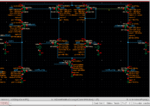
I am designing a 3rd order butterworth bandpass filter whose channel would be 2MHz and between 1MHz and 3 MHz the transfer function derived for the filter is attached with the architecture used to implement, the circuit block is working fine it's response is attached with the circuit itself it consists of 3 stages of OTA-c cells each stage has 3 OTAs, each triangular cell( OTA) is formed of a balanced cascode ota whose circuit is also attached, and the square block is a common common mode feedback circuit between the two middle otas and the last one, I am having a trouble while doing corner simulations, all of them is fine as attached except for the slow slow mode the center frequency has changed from 2 MHz to 1MHz and as you can see the response is no longer flat, I understand that the slow slow operation would change the Vth to be higher which then decreases the resulting current, however what can I do to reverse such operation to reobtain my flat response and correct center frequency?