NikosTS
Advanced Member level 4
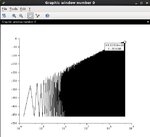
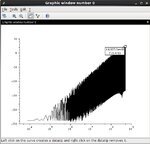
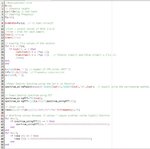
I am trying to plot the power spectrum of the quantization noise for a MASH topology(for frequency synthesizer) , but i have an offset of about 20 dB from the ideal curve.
On a last paper that i read , it was written that the desired power spectrum is given from the output of the SD modulator after removing the dc term.
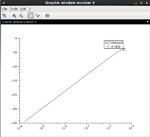
What is the dc term that is mentioned? Is it the mean value of the sequence? ( in the case of frequency synthesizer, the fractional word)
Or just the term at frequency 0?
Thank you in advance,
Nikos
On a last paper that i read , it was written that the desired power spectrum is given from the output of the SD modulator after removing the dc term.
What is the dc term that is mentioned? Is it the mean value of the sequence? ( in the case of frequency synthesizer, the fractional word)
Or just the term at frequency 0?
Thank you in advance,
Nikos