ArdyNT
Full Member level 2
I need to display the LUX on the LCD by using LDR. My problem is in calibration. Actually it can be done by comparing the real LUX meter with my LDR resistance and find the factor. But I don't have LUX meter for now, so I decide to use the following graph which is provided by the datasheet:
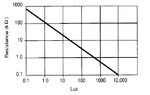
Now, can somebody help me to find the multiplication factor or maybe the equation that shows the relation between LDR resistance (y-axis) with LUX (x-axis). I really have a problem with this logarithmic graph. Help please....

Now, can somebody help me to find the multiplication factor or maybe the equation that shows the relation between LDR resistance (y-axis) with LUX (x-axis). I really have a problem with this logarithmic graph. Help please....