Why a Diamond buffer?

[oneoldude]

I have been reviewing web posted discrete designs for output buffers for headphone amplifiers.

For discrete circuits it seems there is an overwhelming favorite. It is the Diamond buffer. I cannot see why it is favored over the common Complementary Symmetry PP topology. Perhaps someone can explain.

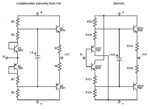
The schematic below shows two common, simple but functional versions of the two buffers.

The cap in each circuit is as suggested by Jung and in my simms that cap does a great job at reducing distortion in Class A mode. If either circuit will spend considerable time in Class B, an additional cap can be placed from the top of R5/R105 to the bottom of R6/R106. This will improve distortion in the Class B region. I do not want to go there so I have not included those caps.

It seems to me that the CSPP is better suited for discrete construction. Thermal feedback in the CSPP is between identical transistors, NPN to NPN, PNP to PNP. They are easy to match for diodic equivalency if you wish and of course the bias of the drivers is set by the diode junctions of identical transistors that are thermally connected.

The Diamond on the other hand has its output transistors biased by unlike transistors, NPN to PNP and PNP to NPN. These are much harder to match if you wish. Also, I have seen Diamond circuits on the net where the thermal feedback is NPN to NPN and PNP to PNP which makes no sense to me because the thermal feedback is not directed to the actual transistor that provides bias to a given output transistor. Indeed, I have seen circuits where the current in the bias transistors significantly exceeds the current in the outputs (a bit much if you ask me even for a current mirror) and each transistor is on a separate HS with no thermal feedback at all.

Am I missing something? What is it that makes the Diamond circuit favored over the CSPP in discrete designs? Is it higher and stiffer input impedance? Or is it the name?

I have simmed both circuits and both result in all distortion products down more than 120 dB with outputs biased at 25 mA and the buffer inside the feedback loop. The Diamond is a couple dB better though. As far as I can see they are virtually identical. With 25 mA Ic in the outputs, and a supply of +- 9V or more, it seems both circuits will supply sufficient current and voltage to fully power headphones with impedances from 30 to 300 ohms before crossing to Class B mode with low impedance phones. I know that a sim beggs reality but I am comparing apples to apples.

So, my two questions:

1. Why the Diamond buffer over the CSPP in a discrete design?

2. Shouldn't the temp compensation in a discrete Diamond be from bias transistor to output transistor NPN-PNP for proper temp stability?

Well, here are the example circuits and thanks for any help you can give.

 

[schmitt trigger]

Your analysis is very thorough and well done.

However....For close to two decades, I contributed to Audio Amateur Publications and kept a close working relationship with its late Editor and Publisher, Ed Dell.

As such I know that when dealing with audiophile grade circuits, measurements and simulations are only considered a first-down scenario, and many further circuit tweaks and refinements are solely based on listening comparisons.
In other words, audiophile circuit design it is both a science and an art.

Walt Jung is one of those rare individuals who is a both a superb engineer and skilled craftsman with respect to audio design. Many of the things he did I did not fully agreed or understood, but when I actually built them I was pleasantly surprised with the results.

Have you lurked around DIYaudio.com? They have all sorts of discussions on topics like these.

 

[dick_freebird]

The "diamond" buffer has the advantage of a higher
input impedance, letting your preceding gain stage
do its work without degrading the gain (via parallel
Rout).

A "complementary bipolar" process will be designed
with some aims being roughly-matched NPN and PNP
Vbe-for-Ic, roughly-matched Hfe-for-Ic so that the
"unmatched" devices will match well enough to make
these sorts of circuits work out.

A cheeseball lateral NPN vs substrate PNP, well, that
has no place in audio dynamic circuitry. You have to
pick the right horse.

 

[BradtheRad]

I am running simulations of both schematics. I also find that performance appears similar.

So I tried reducing the supply rails to +- 1.2 V (as though we wanted to make the project compact by using two rechargeable cells). By reducing headroom, it can bring out shortcomings.

I replaced R1-R2 (and the other resistor networks) with potentiometers. The goal is to adjust bias/signal ratios so as to obtain optimum efficiency.

My observations:

* The second schematic can tolerate a wider variation of pot settings and still operate properly. The first schematic requires careful adjustment of the pots.

* The second schematic can be driven by smaller input current. Thus it can make do with higher impedance in the preceding stage (known and unknown).

 

[oneoldude]

Thanks for the input guys.

I have reviewed the web for headphone amp designs and found a motley collection of circuits out there. Some are unable to supply sufficient current for low Z phones. Others cannot supply sufficient voltage for hi Z phones. Some have no CMRR or PSRR. Some violate the rules of thermal feedback and heat sinking. Others supply obscene amounts of current that seem unnecessary to me. And some are so complex as to border on the ridiculous rather than the sublime.

So I am down to 4 choices. All of them basic, simple and straightforward with no: protection circuits; relays; LCD displays; remote or motorized volume controls; crossfield; battery power; etc. But with a well regulated supply.

They are:

an OPA followed by a CSPP;

an OPA followed by a Diamond;

an OPA followed by paralleled OPAs like the Burr Brown current doubler (the O2);

https://www.ti.com/lit/an/sboa031/sboa031.pdf

https://www.intersil.com/content/dam/Intersil/documents/an11/an1111.pdf

https://nwavguy.blogspot.com/2011/07/o2-headphone-amp.html

or an OPA followed by paralleled OPAs like the Doug Self amp but with way fewer OPAs.

https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&cad=rja&ved=0CCoQFjAA&url=http%3A%2F%2Fwww.vegalab.ru%2Fforum%2Fattachment.php%3Fattachmentid%3D126714%26d%3D1308673533&ei=1q9hUqWUM4Ha9QTlo4CIBg&usg=AFQjCNFq12sEi5UmIkHP5S7ZUruaCoRj6w&sig2=kFf5iaMu5s9uTbU9sOUiyg&bvm=bv.54934254,bs.1,d.eWU

I suspect that all of these topologies, if well implemented on a proper PCB, will sound exactly the same. The only question will be ease of construction, temp compensation on discretes and PCB layout.

So, anyone willing to share their single sided PCB designs for any of these 4 versions? I need single sided because I make my own PCBs and do not have multilayer capability. You can post here or PM me.

Thanks