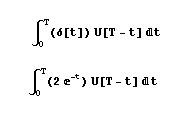aryajur
Advanced Member level 3
- Joined
- Oct 23, 2004
- Messages
- 793
- Helped
- 124
- Reputation
- 248
- Reaction score
- 37
- Trophy points
- 1,308
- Location
- San Jose, USA
- Activity points
- 7,788
Attached are 2 integrals for convolution. Please share your solutions for this. I think I am not getting the correct answers. Thanks.