mayd85
Junior Member level 3

- Joined
- Apr 10, 2013
- Messages
- 30
- Helped
- 3
- Reputation
- 6
- Reaction score
- 3
- Trophy points
- 1,288
- Activity points
- 1,505
Hi,
I am trying to calculate the RMS current through a MOSFET for the sake of calculating its power dissipation. The MOSFET is acting as a low side driver with an inductive load. Now most of the app notes and articles out there model the inductor current as ramp for calculations. This is ok for high frequencies of switching (in KHz). But I think for low frequencies (say 100Hz) the exponential nature of inductor current must be considered. Otherwise, we would underestimate the current, especially for higher duty cycles. Therefore, I tried to calculate the RMS current using standard RMS current formula using integration.
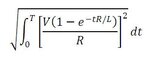
I evaluated the integral in this formula. But when i plug in the actual values, the term under square root goes negative. I don't know whether I am evaluating the integral incorrectly or I am approaching this whole thing in the wrong way. Any help would be highly appreciated. If there is any other way of calculating the RMS current, that too would be helpful.
I am trying to calculate the RMS current through a MOSFET for the sake of calculating its power dissipation. The MOSFET is acting as a low side driver with an inductive load. Now most of the app notes and articles out there model the inductor current as ramp for calculations. This is ok for high frequencies of switching (in KHz). But I think for low frequencies (say 100Hz) the exponential nature of inductor current must be considered. Otherwise, we would underestimate the current, especially for higher duty cycles. Therefore, I tried to calculate the RMS current using standard RMS current formula using integration.
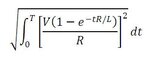
I evaluated the integral in this formula. But when i plug in the actual values, the term under square root goes negative. I don't know whether I am evaluating the integral incorrectly or I am approaching this whole thing in the wrong way. Any help would be highly appreciated. If there is any other way of calculating the RMS current, that too would be helpful.

