Fovakis
Member level 5
- Joined
- Nov 15, 2012
- Messages
- 88
- Helped
- 1
- Reputation
- 2
- Reaction score
- 1
- Trophy points
- 1,288
- Location
- Greece,Athens
- Activity points
- 2,028
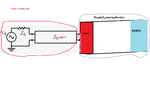
Hello, i am new here in the forum. I have one question on CST Microwave Studio. . So i have a restrangular waveguide with e=5 μ=1. I use a waveguide port to put energy. I want to estimate the charasterist impedance Zo. I think that this must be 50 Ohm for most of RF circuts. So i have |s11|=0,62 and magnitude Zmatrix(1,1)=300. So we have s11=Zload-Zo/Zload+Z0=>
Zo=70 Ohms. So i am wrong. Then i went to transient solver and i put normalize to fixed impedance 50 and adaptive mesh refinement. I run again and s11=0,97 Zmatrix(1,1)=257 so, Zo=3,91 !!!!!!!!!! I thougt that now it should be 50 Ohms. I don't know what is wrong. I have 30 lines per wavel and 30 lower mesh limit at mesh properties.
Friendly George
Zo=70 Ohms. So i am wrong. Then i went to transient solver and i put normalize to fixed impedance 50 and adaptive mesh refinement. I run again and s11=0,97 Zmatrix(1,1)=257 so, Zo=3,91 !!!!!!!!!! I thougt that now it should be 50 Ohms. I don't know what is wrong. I have 30 lines per wavel and 30 lower mesh limit at mesh properties.
Friendly George