omerysmi
Member level 5
Last edited by a moderator:
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
I didn't explain myself very well but i can't edit the post now, so i will explain again:The description isn't particularly clear, but I believe you need three states. The present state machine detects odd number of zeros.
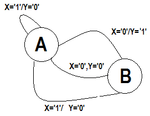
O.K., different problem, different solution.
But in your example a single zero considered as a block of zeros because after the first zero Y is '1'..The statement "block of zeros" would imply that 1 zero is not a block of zeros and that the block is atomic so only when the block is complete do you detect if it's odd or even. You should clarify this requirement.
At the moment the FSM you've proposed won't work (using my assumptions) as it flags all odd instances of 0 in a block of 0's.
e.g.
X=100000010001
Y=010101001010
You need four states where...
State1 (initial, or one): start with assuming input is 1 (initial state)
stay in this state until input is 0 and go to first zero state.
State2 (first zero): either go to state1, if a '1' shows up, or go to state 3 if a '0' shows up (even zeros)
State3 (even zero): either go to State1, if a '1' shows up (means the block of 0's is an even count), or if a '0' shows up then go to state4 (odd zero).
State4 (odd zero): either go to state1, if a '1' shows up and output a 1 on Y to indicate and odd number of zeros, or if a '0' shows up then go back to state3 (even zero)
If you are supposed to detect singleton '0's then get rid of state4 and adjust the Y output to go active when exiting state2 back to state1, and send state3 back to state2 instead of state4.
Of course this is probably a homework assignment so I probably should not have given such a detailed answer....
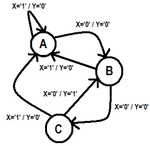
1. to wait until '1' will appear and then to see if the block was even or odd (but there is a problem because '1' could also not appear in the end like "1101000"