dxt78
Newbie level 4
Hello,
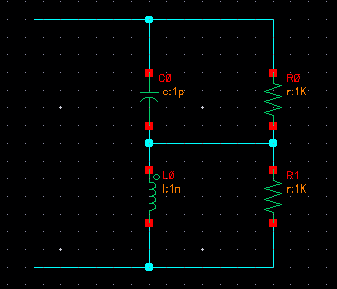
I have an RLC tank as shown in attachment (2R in parallel with an L and a C). I have two questions about it:
1) Why is the characteristic impedance of this LC tank sqrt(L/C) and what meaning does it have?
2) When computing the input resistance of this tank, what role should the characteristic impedance play?
Thanks.
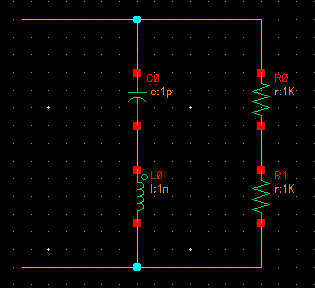
I have an RLC tank as shown in attachment (2R in parallel with an L and a C). I have two questions about it:
1) Why is the characteristic impedance of this LC tank sqrt(L/C) and what meaning does it have?
2) When computing the input resistance of this tank, what role should the characteristic impedance play?
Thanks.