Hexagonal EBG structure dispersion diagram with CST

[pitchoh]

Hi all I'm new to the forum,

I'm working on my final bachelor thesis and I'm supposed to draw the dispersion diagram of a structure composed by two infinite parallel PEC planes filled with PEC cylinders arranged in an Haxagonal lattice.

This Structure PBS is supposed to present a pair of Dirac Cones at the K symmetry point of the Brillouin Zone, but none of my simulations seems to go even close to this point. I'm working with CST, and I tried several cells, is there something I'm doing wrong? Is it possible that CST isn't able to resolve non-squared geometry periodic structures? I'm very concerned...

the results I should obtain are the ones in fig 1.b in "guiding electromagnetic waves around sharp corners: Topologically protected Photonic Transport in Metawaveguides" by Tzuhsuan Ma.

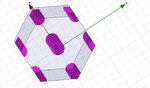
I post the last unit cell I've tried to simulate.
View attachment dispersionnew.zip

EDIT: The results obtained to this point are the ones in figure where "1" stays for K point and "2" stays for M point:


Thanks to all

 

[PlanarMetamaterials]

Welcome pitchoh,

I'm not familiar with hexagonal unit cells, and I don't have CST, but have you ensured that your structure is identical to the one in the paper? The orientation of the curves near the K-point seem to suggest a large physical discontinuity somewhere.

Good Luck

 

[pitchoh]

If the periodic condition in CST is geometrically equivalent to the "unit cell" condition yes, they should be. Meybe CST can't handle a PEC surface on a periodic boundary, this is the unit Cell I draw:

 

[PlanarMetamaterials]

Hi pitchoh,

Owing to the fact that your unit cell has four sides, I don't think it will represent a hexagonal lattice. Your geometry does not seem to be the same as specified in the paper.

 

[pitchoh]

Hi PlanarMetamaterials,

thank you for your replies I also think that probably there is something wrong with the geometry, but CST only allows me to draw four sided unit cell, HFSS (if you're more familiar with it) instead permits to draw whichever unit cell but I don't know how to set up the phase shift of the three couple of boundaries (for an Hexagonal lattice) to sweep over the brillouin zone, do you have any suggestions for this?

I've drawn this unit cell in Hfss


and setted the opposite boundaries as 3 Master-slave periodic couples, but handling the three pase shifts seems to be somewhat tricky...

thank you

 

[PlanarMetamaterials]

Hi pitchoh,

Yes, I use HFSS. Your use of Master-Slave boundaries sounds correct; the G-M region will then be the case where two of the pairs have a 0 degree phase shift, and the third is swept from 0 to 180 degrees.

The M-K region will then be determined by sweeping one other face pair's phase shift from 0 to 180 degrees, while holding the original one at 180 degrees.

Alternatively, you should be able to obtain the G-K region by sweeping two of the faces from 0 to 180 degrees, while holding the third at 0 degrees.

Note: this is speculation on my part, you'll need to verify. I'm looking at the hexagonal system at https://en.wikipedia.org/wiki/Brillouin_zone

Good Luck