help required for implementing in fpga

[vishnu36]

I have task of decoding the position signal from resolver/encoder quadrature outputs. I have used angle tracking observer algorithm method to decode the angle theta in matlab. I want to convert it to fixed point from first principles( not using matlab fixed point advisor) for FPGA implementation. The algorithm requirement is shown below:

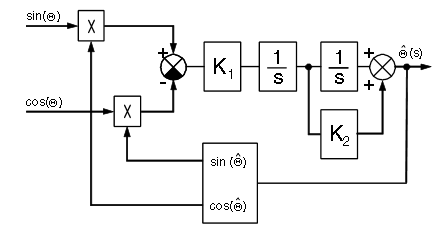
The range of sine/cosine theta is 0-5Vpp. How should I decide the fixed point sizing of the above elements and successfully implement it in FPGA. I had used AN3943 for my understanding of the algorithm.

 

[FvM]

Quoted AN3943 is a DSP application note dedicated to NXP MCP5500 series. It has an internal ADC, but your FPGA most likely hasn't. So the first question is, what's your intended ananlog interface?

Fixed point arithmetic solution will be chosen according to ADC resolution and required precision, I would expect something between 12 and 16 bit.

 

[vishnu36]

Hi FvM

I intend to use AD7606 bipolar ADC, 16 bit for sampling quadrature signals.

 

[FvM]

Looks good. Fixed point arithmetic can be implemented with fixed point VHDL package or as signed arithmetic with implied scaling factor. You'll also need to implement sine/cosine tables.

 

[vishnu36]

Can you guide me further. How to choose the Q point for PI controller , Integrator and particularly sine/cosine generator?
Can I use taylor series to implement sine/cosine ( as it is valid for 4 quadrants)?

 

[FvM]

Scaling is quite obvios for some signals and parameters, e.g. sine generator. For others, it can be best figured out with a simulation of the algorithm, e.g. in Matlab.

Taylor series (polynomial approximation) of sine function isn't effective for full range, better use table with linear interpolation.

 

[vishnu36]

Hi FvM

I tried 7th order polynomial approx for sine/cosine and it works very well in simulation (floating point). The only problem is that input range to taylor cannot exceed the range -pi to +pi. In the ATO implementation, P+I stage accumulates beyond 3.14 , when simulating for velocity. How can we restrict P+I controller to roll off beyond 3.14 and start from 0 again?

 

[barry]

i’m not sure I understand. Why would you want the output to ‘roll over’ from 3.14; don’t you want it to saturate?

 

[vishnu36]

if it saturates at after 3.14 then the algorithm fails to converge for velocity inputs. The instantaneous value of sine/cosine generator must match with the input quadrature signal rate in order to provide error free output.

 

[FvM]

Set up HDL code for 7th order sine approximation, simulate it and come back...

 

[vishnu36]

FvM
I am trying but I really wanted a clue of fixing Q point for the logic

 

[Akanimo]

Q = 1/(2*damping factor)

--- Updated Jun 9, 2022 ---

Can you guide me further. How to choose the Q point for PI controller , Integrator and particularly sine/cosine generator?
Can I use taylor series to implement sine/cosine ( as it is valid for 4 quadrants)?

There are several references to the document that you quoted. Did you also look at the referenced documents?

 

[FvM]

With Q, OP refers to fixed point position (2^n scaling factor). To answer the question, you need to analyze the range of each parameter and variable in your calculation. To save redundant bits, it's not unusual to use different scaling for each parameter. As saturation logic is no default feature of most FPGA and needs additional logic resources, you should also determine at which places numeric overflow may occur and handle it respectively.

--- Updated Jun 9, 2022 ---

I see that scaling of variables is also discussed in AN3943, the angle accumulator apparently wraps around at +/- 1.

 

[vishnu36]

Hi FvM

Referring to AN3943, if I could scale my inputs in the range -1 to +1, then Q15 format would be ideal. Now the real question is to fix the Q format for multiplier, accumulator/controller, and trig functions. I decided to go for CORDIC due to ease and precision. The difficulty is that I am unable to understand how angle accumulator gets wrapped up in the range -1 to +1. In that case angle accumulator should be Q15, which is highly unlikely. Kindly clarify

 

[FvM]

+/- 1 range and wrap around can be seen in the timing diagram. I don't understand why it should be unlikely. Of course +/-1 corresponds to +/- pi in rad.

 

[vishnu36]

FvM

My understanding is that beyond +/-1 , accumulator should overflow in order to wrap up. In that case should it be Q15?

 

[FvM]

Yes. Notice that both, second integrator (accumulator) and adder with K2 term need wrap around behaviour. For the first integrator, I would rather expect saturation behaviour. If you have access to the MCP5500 code, you can check how it's exactly implemented.

 

[vishnu36]

Hi FvM
I tried in matlab with partial success. Few more inches to get to the target. I modeled the entire system using ADC quantizer and the outputs(int16) were connected to the algorithm (mimics the actual behavior). In my model i scaled the int16 of sine and cosine to (+/-1 V level) and algorithm performed correctly.
Then I used fixed point advisor to convert the model from float to fixed. here I was stuck up. ADC outputs are fixdt(1,16,15) and for rest of the model, the advisor assigned the scaling automatically . After simulation I found the behaviour erratic. Tried several times but with less luck. any advise of how to solve this problem?