KlausST
Advanced Member level 7

Hi,
It is an undefined value. Impossible to "find" it in a mathematical way.
In your case it is I(0). The current through the coil at the beginning of the process.
Mathematics can not know what this value is.
Klaus
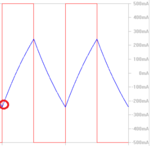
Here I see the problem.I want to find the IntegrationConstant
It is an undefined value. Impossible to "find" it in a mathematical way.
In your case it is I(0). The current through the coil at the beginning of the process.
Mathematics can not know what this value is.
Klaus