Echo Cancellation Question...

[mshaw]

Hi,

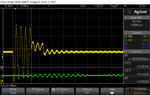
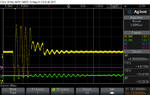
Fairly new to this so please be gentle! I'm looking for advice/clarification more than a specific answer. Referring the the image attached we have an input signal (red) which is pulsed into a steel pipe (approx. 3m in length), the output signal is measured and is shown in blue. My job is to detect the input signal which is 'embedded' within the output signal.



I have a few questions...

1) Am I seeing echo's in the output data?
2) I've done a fair amount of reading an I believe I may be able to run some Echo Cancellation to retrieve the input signal?

I'm comfortable with the Math's and concepts of Convolution, etc. I've never actually done this in 'real' before so I'm just asking for some basic pointers if anyone can help.

Thankyou,
Mike.

 

[KlausST]

Hi,

Did you try a mathematical correlation?

Klaus

 

[mshaw]

Hi,

Did you try a mathematical correlation?

Klaus

Hi,

Yes, I can run FFT Analysis to determine the frequency of interest and use a correlation function to detect the input signal. What I'm looking for is a way to 'remove' the echo and leave me with the input signal on it's own (or as close to that as possible). At the moment the pipe is stationary, however, there will be times when the system is moving and I'm looking for a way to adaptively extract the input signal. I believe the way forward is Echo Cancellation via a FIR filter but as I'm new to this I was just wondering if that was the correct way forward

Thankyou,
Mike.

 

[Tim876]

Building a good AEC that can follow changing echo path is a relatively complex task. Why not try and either use an open source solution (like Speex) or a commercial solution (like SoliCall) ?

 

[FvM]

Referiing to your problem specification, what does "detect the input signal which is 'embedded' within the output signal" exactly mean?

The shown output waveform suggests that the transfer function of the system can be decompensated into the basic transfer function and a repeated echo. The output of the basic transfer function without the echo is roughly what you see up to the first envelope minimum, ignoring the smaller response to the negative input step.

So quite obviously, the basic transfer function involves a small band filter that broadens burst response to a more gaussian envelope. Due to the small band excitation signal, it's not possible to derive the transfer function unequivocally without additional assumptions.

 

[KlausST]

Hi,

Usually you should know your input signal, therefore running the FFT is redundant.
Determine the frequency of interest: in my eyes is not necessary for running a correlation.

Just run the correlation between input and output signal.
The result of the correlation should give the coefficients of the FIR filter (just with inverted sign)

Can you show us the results of the correlation?

In your diagram the horizontal line is "samples". Please show it in "time" or give the sample rate.

Mind the echo of an open pipe is "negative", and of a closed pipe is "positive".
Expect the first echo of a 3m pipe after about 20ms..

Klaus

 

[mshaw]

FvM,

Thankyou for that. What I was meaning in my statement "detect the input signal which is 'embedded' within the output signal" was that I wondered if it is possible to take the Output signal (echo, etc) and perform an AEC method to retrieve the original input signal.

To verify my understanding of your post, the Input Signal (4 cycle @ 2600Hz) is pulsed into the Pipe. There is then a corresponding Transfer Function for the system that takes the Input and produces a Gaussian Envelope. It is this Gaussian Envelope that is echoed.

When you say that the Basic Transfer Function involves a Small Band Filter that broadens the burst response - I think it is this Small Band Filter that I am trying to find...

I've read a number of Papers that suggest that the Output Signal = Input Signal * FIR Filter + Gaussian Noise - where * is convolution.

I guess I thought I could adaptively change the FIR co-efficients to allow me to retrieve the original signal - but I also guess it's harder than I first thought... What I can't 'see' is how to establish the FIR filter in the first place.

I hope I'm making sense. It's the first time I've looked at this problem so although my Math is ok it's 'visualising' the Math that I'm struggling with!

Thankyou,
Mike.

 

[mshaw]

Hi,

Usually you should know your input signal, therefore running the FFT is redundant.
Determine the frequency of interest: in my eyes is not necessary for running a correlation.
Just run the correlation between input and output signal.

I agree totally, the FFT part is really for my testing/verification. I have a Mathcad worksheet where I split the output signal into chunks and window/zero pad for further anaylsis but I agree I don't actually need to do that in realtime.

The result of the correlation should give the coefficients of the FIR filter (just with inverted sign)
Can you show us the results of the correlation?

In your diagram the horizontal line is "samples". Please show it in "time" or give the sample rate.

Mind the echo of an open pipe is "negative", and of a closed pipe is "positive".
Expect the first echo of a 3m pipe after about 20ms..

Klaus

What I can probably do is to put together a few screenshots from Mathcad/Scope that show the Time Domain and what I am trying to achieve.

The result of the correlation should give the coefficients of the FIR filter (just with inverted sign)

Really interested in this statement. Do you have any examples you could point me to? When I say I perform a correlation, I correlate between the Input Signal (4 cycle @ 2600Hz) and the Output signal. The correlation function just returns a single value, i.e. 1 for a perfect match to 0 for no match and -1 for a perfect (inverted) match. So if my Input Signal is 4 * 9 samples = 36 samples I correlate against 36 samples of the output signal to find as close to 1 as possible. Hope this makes sense.

 

[KlausST]

Hi,

You should not not correlate with only 4 sampmes, but with the whole sequence ( of interest) with the output signal.
As far as ican see this are about 100 samples of input signal.

And you have to correlate it with the output signal. For tis is maybe 500 samples in length you need to correlate sample 0 to 99 of output signal with the input signal, then 1...100, then 2 to 101 up to 400 to 499 .
This gives 400 outputs for the correlation.

Then show these 400 values in a diagram...

Klaus

 

[FvM]

I think you should distinguish two questions:
1. What's the principle way to calculate an inverse transfer function that retrieves the input signal?
2. Can you expect to retrieve the input signal of the shown output signal under real conditions?

As far as I see, there's a solution for 1. if the output signal is bounded. But looking at the small band transfer characteristic, it's effectively impossible to retrieve the original input signal with only small amounts of noise are added to the output.

 

[mshaw]

Thankyou for the replies. I will put together a document with Time Domain, etc and post. For now though, the attached below shows what I was thinking.



What I have done is to take the Input and also the Output up until it starts to echo (I think this is correct). I have then Deconvolved the signals to give what I think is the Transfer Function (the filter I alluded to above). Using this, I can extract a close representation of the Input signal to correlate against.

My process may well be incorrect as it's all new, but the general idea of what I'm trying to achieve is in the image above.

My thinking was that if I can remove the Echo, I could Deconvolve the Output signal (the first Gaussian Envelope) and extract the original signal to correlate against... But I may be wrong!

Thankyou,
Mike.

 

[mshaw]

Hi,

You should not not correlate with only 4 sampmes, but with the whole sequence ( of interest) with the output signal.
As far as ican see this are about 100 samples of input signal.

And you have to correlate it with the output signal. For tis is maybe 500 samples in length you need to correlate sample 0 to 99 of output signal with the input signal, then 1...100, then 2 to 101 up to 400 to 499 .
This gives 400 outputs for the correlation.

Then show these 400 values in a diagram...

Klaus

I will do this and Post, thankyou.

 

[mshaw]

I will do this and Post, thankyou.

Ok, I hope the following makes sense.

This first image is a Scope capture of the Input (yellow) and the Output (Green). You can see that this is a timeframe of 10 milliseconds and I've placed the X1 and X2 cursors to show the time of the Input Signal - 1.55 milliseconds.



This next image shows what I think is the timeframe of the Output Signal - 5.88 milliseconds.



The sample rate of the Scope is 5MSa/s, however, I have saved off the data at a sample rate of 1/(0.01/2000) = 200KSa/s.

The following shows the data within Mathcad:



The following is a repeat of the Convolve / Deconvolve above:



And finally, here is my step through of the Correlation as suggested above and the graph of the correlation values - note that the COR vector are the Corrleation values. I have ran a Convolution between the Input function and the COR vector which replicates the Output function - which is great although I don't fully understand why it is so.



As previously mentioned, I'm more interested to hear that I am doing the right thing and if I'm not what should I be doing to detect the input signal.

Thankyou for your help/guidance, it is appreciated.