righteous
Full Member level 2
Gents,
The question is; why do a load on the secondary winding result in increased current in the primary winding on some transformers? (or maybe all, I don't know.)
I have this question, because as I have been taught, the only coupling between primary and secondary is the flux in the core, and it is the primary that determines the amount of flux. At least this is how it is presented in textbooks :
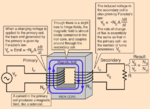
So if the only coupling is flux, is the increased current in the primary due to a badly designed transformer with mutual induction? Or are there another feedback (sec -> pri) mechanism in a transformer?
- - - Updated - - -
Never mind, I found some sort of answer here:
http://electronics.stackexchange.com/questions/169129/flux-in-transformers
The question is; why do a load on the secondary winding result in increased current in the primary winding on some transformers? (or maybe all, I don't know.)
I have this question, because as I have been taught, the only coupling between primary and secondary is the flux in the core, and it is the primary that determines the amount of flux. At least this is how it is presented in textbooks :

So if the only coupling is flux, is the increased current in the primary due to a badly designed transformer with mutual induction? Or are there another feedback (sec -> pri) mechanism in a transformer?
- - - Updated - - -
Never mind, I found some sort of answer here:
http://electronics.stackexchange.com/questions/169129/flux-in-transformers