chiques
Full Member level 3
- Joined
- Nov 21, 2007
- Messages
- 168
- Helped
- 2
- Reputation
- 4
- Reaction score
- 2
- Trophy points
- 1,298
- Location
- California
- Activity points
- 2,534
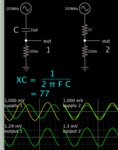
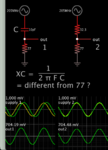
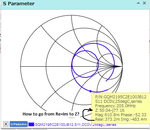
How do I convert 50.04-j77.16 on a 50 Ohm Smith Chart to a capacitance value of 10.1pF?
Using GQM2195C2E100JB12
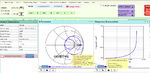
Using GQM2195C2E100JB12