Lupifieri
Newbie level 3
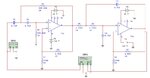
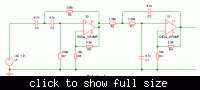
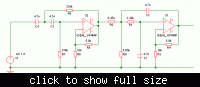
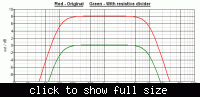
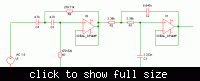
Good Morning, I am struggling to modify a Butterworth filter between 100Hz and 10kHz and unit gain (0dB), I know that to calculate the gain, the formula is G=1+Rf/Ri, the problem is that to achieve 0dB, I need a total gain =1, to have the total gain=0dB (20log(1)), I need 0.5 on each side... how can I add a number to 1 and get 0.5 as answer? Can someone PLEASE help me?
Attachments
Last edited: