Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
The Resonators are identical and if the coupling is tight, I think this is normal.
It looks like a coupled LC Resonators..
SunnySkyguy said:What Q's and coupling coefficient did your expect? Your equivalent BW= 125 MHz averaged at 2153 MHz (but asymm.) results in a Q of 17.
You may compute the Q from each outside skirt and then the coupling factor as said before with any double tuned coupled resonator equiv cct. depending on Q and spacing of f1,f2. The phase response may be more sensitive or accurate for this calc..
Input and output ports must be very weakly coupled to the resonators.
See also examples in the book "Microstrip Filters for RF/Microwave" (Hong/Lancaster).
View attachment 154836
View attachment 154837

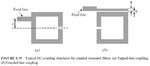

I can't get the sharp peak shown in figure 8.16. any ideas ?
Those are really high Q resonators. Maybe your conductor losses and/or substrate losses are too high, so that possible Q is too low.
I have simulated that resonator in AXIEM and found that the resonator coupling gap has reverse effect compare to standard ones.
View attachment 154939View attachment 154940View attachment 154941