pancho_hideboo
Advanced Member level 5
- Joined
- Oct 21, 2006
- Messages
- 2,847
- Helped
- 767
- Reputation
- 1,536
- Reaction score
- 733
- Trophy points
- 1,393
- Location
- Real Homeless
- Activity points
- 17,490
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
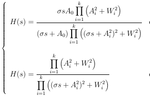
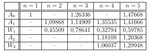
I think they are opposite.The odd order polynomials has only complex poles,
while even number has an additional real pole.
Why does top(odd order case) have zero at s=0 ?The general formula is as follow (top is odd order, bottom even order):
I can calculate Taylor series expansion of exp(p^2), as eq. (13-73) in start of this thread by MATLAB.For higher order I am not sure whether there is a simple values for poles.
Try to look implement above, maybe it is what you need?
function [z, p, k] = my_gaussianap(order, wc, Ac_dB)function [z, p, k] = my_gaussianap(order, wp, Ap_dB)
s = tf('s');
T2 = 0;
for n = 0:order
T2 = T2 + (-1)^n * s^(2*n) / factorial(n);
end
z = zero(T2);
p = z( find(real(z) <= 0.0) );
z = [];
k = polyval(poly(p), 0);
s21 = zpk(z, p, k);
[wc, fval] = fzero(@(wc) dbv( freqresp(s21, wc) ) + Ap_dB, 1.0);
fprintf(1, 'order=%d, ', order);
fprintf(1, 'wc=%g, ', wc);
fprintf( 1, 'Ac_dB=%g, ', -20*log10( freqresp(s21, wc) ) );
z = (wp/wc) * z;
p = (wp/wc) * p;
k = k * (wp/wc)^( length(p)-length(z) );
s21 = zpk(z, p, k);
fprintf(1, 'wp=%g, ', wp);
fprintf( 1, 'Ap_dB=%g\n', -20*log10( freqresp(s21, wp) ) );