Luca_Romano
Junior Member level 2
Hi everyone,
I'm using a 2D Music algorithm for the estimation of Range-Azimuth info in a ULA FMCW MIMO radar.
The algorithm procedure is pretty simple (see "Belfiori F., Application of 2D MUSIC Algorithm to Range-Azimuth FMCW Radar data" or " Manokhin G., MUSIC-based algorithm for range-azimuth FMCW radar data processing without estimating number of targets"). I have some doubt with regard the application of the 2D FB spatial smoothing in order to decorrelate the covariance matrix of the data; I'm wondering if I do some error in the following code section (in the way I order the x_win_new vector):
so in my case I'm scanning the full 2D [NxM] matrix in this way:
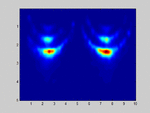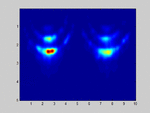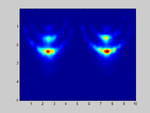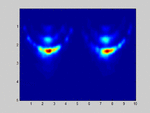
If I select m1=M and m2=N (so no spatial smoothing, only forward/backward averaging) I get good results as shown in the attached image.
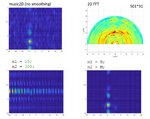
Thanks a lot in advance,
Best regards,
I'm using a 2D Music algorithm for the estimation of Range-Azimuth info in a ULA FMCW MIMO radar.
The algorithm procedure is pretty simple (see "Belfiori F., Application of 2D MUSIC Algorithm to Range-Azimuth FMCW Radar data" or " Manokhin G., MUSIC-based algorithm for range-azimuth FMCW radar data processing without estimating number of targets"). I have some doubt with regard the application of the 2D FB spatial smoothing in order to decorrelate the covariance matrix of the data; I'm wondering if I do some error in the following code section (in the way I order the x_win_new vector):
Code:
x= DataV'; %Data collected by the ULA (31 Spatial samples-31Antennas), 501 time samples
N = size(x,1); % Number of antennas
M = size(x,2); % Number of samples in fast-time dimension
% window dimension for the smoothing dim[m1xm2]
m1 = 25;
m2 = 300;
p1 = N-m1+1; %positions in the spatial dimension
p2 = M-m2+1; %positions in the time dimension
N_submat = p1*p2; %number of all the possible scan
M_tot = m1*m2;
ind_tot=1;
for p1_ind = 1:p1
for p2_ind = 1:p2
x_win_new(:,ind_tot) = reshape (x(p1_ind:m1+(p1_ind-1),p2_ind:m2+(p2_ind-1)),[1,M_tot])';
ind_tot=ind_tot+1;
end
end
X_win_cor = x_win_new*x_win_new';
X_win_cor_conj = conj(X_win_cor);
J= fliplr(eye(M_tot)); %transition matrix
C=(1/2*N_submat)*(X_win_cor + J*X_win_cor_conj*J); %data smoothed covariance matrix (forward+backward)so in my case I'm scanning the full 2D [NxM] matrix in this way:
Code:
x x x . . x x x . . . . . . . .
x x x . . x x x x x x . . x x x
x x x . . x x x x x x . . x x x
. . . . . . . . x x x . . x x xIf I select m1=M and m2=N (so no spatial smoothing, only forward/backward averaging) I get good results as shown in the attached image.

Thanks a lot in advance,
Best regards,