garvind25
Full Member level 3
Hi,
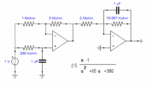
I need to implement a second order transfer function in 's' domain (having 2 poles, 1 zero and 2.5 DC gain) using transistors and discrete components. Since I have not done so previously, can anyone guide me how to do so? I did a search with the keywords ‘realise a second order transfer function, bjt’ but ended up with papers on filters etc.
If possible, pls. point to me to any document / app note/ website demonstrating the transfer function realization with an example.
I am looking forward to your comments.
Thanks,
Arvind Gupta.
I need to implement a second order transfer function in 's' domain (having 2 poles, 1 zero and 2.5 DC gain) using transistors and discrete components. Since I have not done so previously, can anyone guide me how to do so? I did a search with the keywords ‘realise a second order transfer function, bjt’ but ended up with papers on filters etc.
If possible, pls. point to me to any document / app note/ website demonstrating the transfer function realization with an example.
I am looking forward to your comments.
Thanks,
Arvind Gupta.