Yann1000
Newbie level 1
Good evening I have an exercise to achieve, but I'm struggling to terminate the output voltage! I tried to isolate on one side v1 'of the first equation and v2' on the second equation.
Thank you in advance for your assistance
Equation 1: ((v1-v1 ') / R3) + (v2'-v1') / zc1 + (v0-v1') / (2R4) = 0
Equation 2: ((v2-v1 ') / R3) + ((v1'-v2') / zc1) + (v2 '/ (2R4)) = 0
V + = V- that is ((v2') / 2) = (v0 + v1') / (2)
Vo = v2 '- v1'
Vo being the output voltage
We must obtain at the end:
v0 = (- R4) / (R3 + R4) = (v1-v2) / (1 + f / fc) with fc = (R3 + R4) / (4.pi * R3 * R4 * C2)
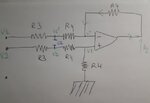
Thank you in advance for your assistance
Equation 1: ((v1-v1 ') / R3) + (v2'-v1') / zc1 + (v0-v1') / (2R4) = 0
Equation 2: ((v2-v1 ') / R3) + ((v1'-v2') / zc1) + (v2 '/ (2R4)) = 0
V + = V- that is ((v2') / 2) = (v0 + v1') / (2)
Vo = v2 '- v1'
Vo being the output voltage
We must obtain at the end:
v0 = (- R4) / (R3 + R4) = (v1-v2) / (1 + f / fc) with fc = (R3 + R4) / (4.pi * R3 * R4 * C2)
