frischling
Newbie level 2
Hello everyone,
I might need your help!!
I have a touchstone file (s4p, S-Paramter) describing a coupling structure including two 'transmission lines'. Now I want to make an eve-odd-analysis using a circuit simulator (ADS). Do you know how to find out the even/odd impedance and the characteristic impedance matrix for the entire structure? The characteristic impedance of one such file is about 58Ohm and almost over the frequency. The system impedance is 50Ohm. How should I terminate the ports to find out the impedances?
Thank you for your help
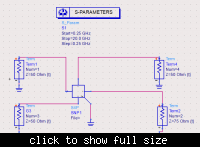
I might need your help!!
I have a touchstone file (s4p, S-Paramter) describing a coupling structure including two 'transmission lines'. Now I want to make an eve-odd-analysis using a circuit simulator (ADS). Do you know how to find out the even/odd impedance and the characteristic impedance matrix for the entire structure? The characteristic impedance of one such file is about 58Ohm and almost over the frequency. The system impedance is 50Ohm. How should I terminate the ports to find out the impedances?
Thank you for your help
